�$BL\
The outline of finite difference method adapted for this model
is as follows.
- Space differencing
-
The finite difference form of governing equations of the model are
considered on the Lorenz type staggered grid.
The space differencing is evaluated by the forth order centered
scheme for scalar advection terms and the continuity equation,
and the second order centered scheme for others.
The numerical diffusion is introduced to the equation of motion,
turbulent kinetic energy equation, and advection diffusion
equation of dust so that the 2-grid noise associated with
central finite differencing can be suppressed.
The numerical diffusion in equation of motion is proportional to
the squared wind shear and that in turbulent kinetic energy
equation, and advection diffusion equation of dust is
proportional to the third power of Laplace operator.
The vertical integral in calculating CO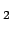 infrared radiative flux is evaluated by the trapezoidal rule.
infrared radiative flux is evaluated by the trapezoidal rule.
- Time differencing
-
The time integration is performed by the leap-frog scheme for
advection and buoyancy terms and the forward scheme for
turbulent diffusion and forcing terms.
The forward scheme is also adapted once per 20 steps for
advection and buoyancy terms to stabilized numerical solution.
The radiative flux associated with dust is given by iteration
method of the matrix equation, where the number of iteration
is 4.
The time integration of 1D thermal conduction equation of grand
surface is performed by the Crank-Nicolson scheme.
In the following sections, the subscripts 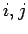 show horizontal and vertical grid point, and the superscripts
show horizontal and vertical grid point, and the superscripts
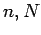 show time step.
The number of vertical grid level is
show time step.
The number of vertical grid level is 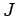 .
The scalar and basic state variables are evaluated on the grid point
and the other variables are evaluated on the half grid point.
.
The scalar and basic state variables are evaluated on the grid point
and the other variables are evaluated on the half grid point.
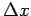 and
and 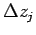 are the
horizontal and vertical grid intervals, and
are the
horizontal and vertical grid intervals, and 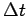 is
the time interval.
is
the time interval.
![]() infrared radiative flux is evaluated by the trapezoidal rule.
infrared radiative flux is evaluated by the trapezoidal rule.
![]() infrared radiative flux is evaluated by the trapezoidal rule.
infrared radiative flux is evaluated by the trapezoidal rule.
![]() show horizontal and vertical grid point, and the superscripts
show horizontal and vertical grid point, and the superscripts
![]() show time step.
The number of vertical grid level is
show time step.
The number of vertical grid level is ![]() .
The scalar and basic state variables are evaluated on the grid point
and the other variables are evaluated on the half grid point.
.
The scalar and basic state variables are evaluated on the grid point
and the other variables are evaluated on the half grid point.
![]() and
and ![]() are the
horizontal and vertical grid intervals, and
are the
horizontal and vertical grid intervals, and ![]() is
the time interval.
is
the time interval.