In the advection diffusion equation of dust (
equation (20) in Part I), the advection term
![]() is evaluated by the forth order centered
scheme and the vertical advection term associated with the
gravitational settling
is evaluated by the forth order centered
scheme and the vertical advection term associated with the
gravitational settling
![]() is evaluated by the first
order upstream scheme.
In time integration, the forward scheme is adapted for the friction
terms
is evaluated by the first
order upstream scheme.
In time integration, the forward scheme is adapted for the friction
terms
![]() ,
,
![]() and the gravitational settling term
and the gravitational settling term
![]() .
Representation of
.
Representation of
![]() ,
,
![]() and
and
![]() are same as those of
(22), (24) and
(42).
are same as those of
(22), (24) and
(42).
| (49) |
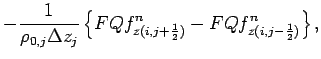 |
(50) | ||
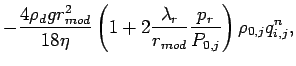 |