|
圧力の診断式 (A.8) を
付録 B.a.i 節
で行った変形にあわせて以下のように変形する.
これを dimension-reduction 法を用いて解く. 上の式を適当に離散化すると,
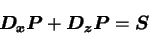 |
(B.19) |
と書くことができる. ただし
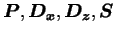 はそれぞれ, はそれぞれ,
を離散化した行列である. 行列 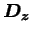 の固有値を の固有値を 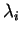 , 固有ベクトルを , 固有ベクトルを 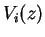 とし, 固有列ベクトルを並べた行列を とし, 固有列ベクトルを並べた行列を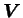 , 対角成分が , 対角成分が 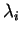 である行列を である行列を
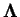 とすると, とすると,
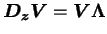 となる. となる.
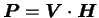 と展開すると, と展開すると,
したがって,
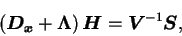 |
(B.20) |
となる.
固有値 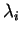 と固有ベクトル と固有ベクトル 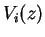 を求めるために必要な を求めるために必要な
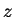 方向の係数行列 方向の係数行列 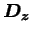 は は
を差分化して与える.
最初の微分は 2 次中央差分, 次の微分は 4 次中央差分で解く.
これは連続の式は 4 次中央差分, 圧力の微分は 2 次中央差分であることによる.
よって係数行列は 5重対角行列になる. 係数行列の成分を 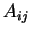 とすると以下のようになる. とすると以下のようになる.
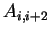 |
 |
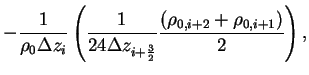 |
(B.21) |
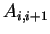 |
 |
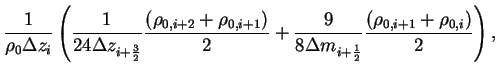 |
(B.22) |
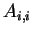 |
 |
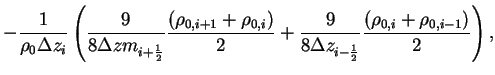 |
(B.23) |
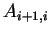 |
 |
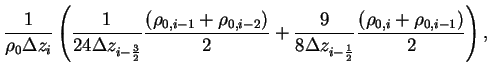 |
(B.24) |
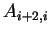 |
 |
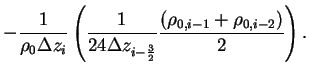 |
(B.25) |
境界条件は上下壁で 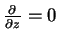 となるようにする. となるようにする.
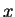 方向についても適当な固有関数に展開して各モードに対する展開係数を求める.
ここでは三角関数で展開する.
方向についても適当な固有関数に展開して各モードに対する展開係数を求める.
ここでは三角関数で展開する.
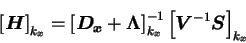 |
(B.29) |
|