順圧ロスビー波の伝播テスト
1 概要
回転系において, 基本場に対してポテンシャル渦度の水平勾配が存在するとき, 水平方向に変位する流体粒子には復元力が働き, ロスビー波 が発生する. 本数値実験では, ポテンシャル渦度の南北勾配が存在する順圧的な基本場に対して微小振幅の初期擾乱を与えることにより, 順圧ロスビー波の伝播をシミュレーションする. そして, 計算された波の位相速度を, 支配方程式の線形近似から得られた位相速度と比較し, モデルの実装の妥当性を確認する.
2 定式化
非粘性な回転系において, 一定の温位を持つ順圧場(物理場が鉛直方向に依存しない場合)を考えよう. このとき, 支配方程式系は流れ関数だけを使ってかける. すなわち, 流れ場の時間発展は, 渦度方程式
\begin{equation} \dfrac{\partial}{\partial t} \nabla_H^2 \psi = - \dfrac{1}{a^2 \cos{\phi}} \left[ \dfrac{\partial \psi}{\partial \lambda} \dfrac{\partial }{\partial \phi} - \dfrac{\partial \psi}{\partial \phi} \dfrac{\partial }{\partial \lambda} \right] ( f + \nabla^2_H \psi ) \end{equation}によって記述される. ここで, \(\psi\) は流線関数である. 回転系特有の波である (順圧)ロスビー波 はこの方程式の解の一つである. 今,
\begin{equation} \psi = Y_n^m e^{i \omega t} \end{equation}の形式の解を仮定し, これを渦度方程式に代入すれば, 順圧ロスビー波の分散関係
\begin{equation} \omega = - \dfrac{2\Omega m}{n(n+1)} \end{equation}が得られる.
3 実験設定
3.1 各実験で共通な設定
- 解像度
- T21L20
- 時間積分
- 時間スキーム: LFAM3
- 状態方程式
- Linear
- 境界条件
- 上端・下端では滑り壁条件
を課す.
- パラメータ
- 惑星半径: 6.371 × 106 [m]
- 自転角速度: 7.292115 × 10-5 [s-1]
3.2 実験間で異なる設定
| 実験名 | m | n | T [hr] | Δ t [min] |
|---|---|---|---|---|
| exp1 | 1 | 1 | 24 | 30 |
| exp2 | 1 | 2 | 72 | 90 |
| exp3 | 2 | 2 | 36 | 90 |
- 時間ステップ幅
- クラーン数が 0.5 以下となるように選ぶ. すなわち \(\Delta t \leq 0.5 \times {\rm min}(\Delta x_{\rm min} / cx_{\rm wave}, \Delta y_{\rm min} / cy_{\rm wave})\).
- ただし, \(cx_{\rm wave} = \omega/(2\pi m/a) = a/(mT), cy_{\rm wave} = \omega/(2\pi n/a) = a/(nT)\).
- 水平解像度 T21 に対して \(\Delta x_{\rm min} \sim 300\) [km], \(\Delta y_{\rm min} \sim 500\) [km] である.
- クラーン数が 0.5 以下となるように選ぶ. すなわち \(\Delta t \leq 0.5 \times {\rm min}(\Delta x_{\rm min} / cx_{\rm wave}, \Delta y_{\rm min} / cy_{\rm wave})\).
- その他の詳細な設定
4 計算結果
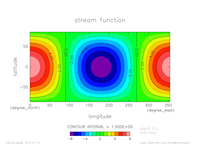
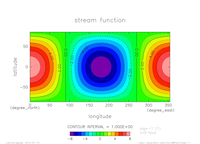
- 流れ関数の時間発展
実験名 アニメーション(中層) (sig=-0.5) 流れ関数(上端) 流れ関数(下端) exp1 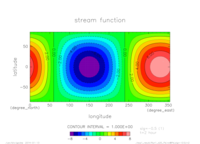
 (lat=0,lon=0,sig=0)
(lat=0,lon=0,sig=0) (lat=0,lon=0,sig=-1)
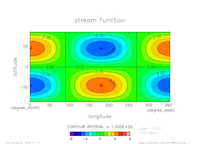
(lat=0,lon=0,sig=-1)exp2 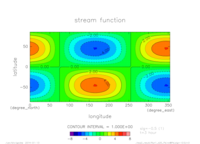
 (lat=45,lon=0,sig=0)
(lat=45,lon=0,sig=0) (lat=45,lon=0,sig=-1)
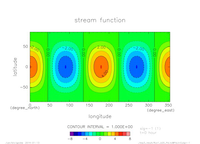
(lat=45,lon=0,sig=-1)exp3 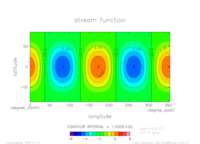
 (lat=0,lon=0,sig=0)
(lat=0,lon=0,sig=0) (lat=0,lon=0,sig=-1)
(lat=0,lon=0,sig=-1)
- 備考
- exp1: \(m=1,n=1, T=24 {\rm [hour]}\)
- exp2: \(m=1,n=2, T=72 {\rm [hour]}\)
- exp3: \(m=2,n=2, T=36 {\rm [hour]}\)