水惑星設定における軸対称な風成循環の数値実験

目次

1 概要

海洋の表層循環は, 海面に吹く偏西風や貿易風の応力によりエクマン層を介して駆動される. 陸の存在する海洋における表層循環の基本的な力学は, 解析的な数理モデル(Stommel, Munk)や数値実験により理解されてきた.

近年, 気候状態に対する大気と海洋の相互作用の仕組みを理解する目的で, 大気・海洋大循環結合モデルを用いた水惑星実験が行われている[4][2]. そこで示された陸のない海洋循環の特徴は岸の存在する場合の循環と大きく異なるため, 両者の間で力学の違いが存在することが示唆されている. また, [2] では, 同等の実験設定を行った水惑星実験にも関わらず, [4] の計算により得られた平衡状態の気候が大きく異なる問題を挙げている. この理由については, [2] は, 海洋モデルの(特に混合過程の)定式化に違いのために, 計算される海洋循環や温度構造, そして海洋の熱輸送が異なるためだと主張している.

水惑星設定における海洋循環もまた気候状態に重要な影響を与えることが予期されるが, 一方で, その循環の基本的な力学は, 陸の存在する海洋循環と比較してまだ広く調べられていない. ここでは,

  • 実装したモデルの妥当性の検証
  • 水惑星設定における海洋循環の基本構造(軸対称構造)の理解

を試みるために, 静止した海洋に対して東西一様な海面応力を与えたとき, どのような循環が駆動されるかを数値実験する.

2 陸の存在しない軸対称な風成循環の力学

(Pedlosky 8.3 節を参考に, 内部領域の解の特徴を記述する予定)

3 実験設定

3.1 ケース間で共通な設定

  1. 計算領域
    • 全球的に広がる水深 \(H= 5.3\) km の海洋. 海底地形や陸は存在しない.
  2. 支配方程式系
    • 静力学ブジネスク方程式
    • 海水の状態方程式
      • 線形(Vallis, 2006)
    • 粘性, 拡散
      • 水平方向の渦粘性, 渦拡散係数 \(A_h,K_h\) の設定
        • 大きさは, 次の各ケース設定を参照.
        • \(A_h\) は \(K_h\) と同じにとる.
      • 鉛直方向の渦粘性, 渦拡散係数 \(A_v,K_v\) の設定
        • 海面流速が [2] と同程度になるように, \(A_v=1.0 \times 10^{-2}\) [m2 s-1] にとる.
        • \(K_v\) は \(A_v\) と同じにとる.
  3. 境界条件
    • 海面応力
      • [2] における準平衡状態での地表風速から計算された, 海面応力の東西平均場を与える.

      \[ \rho_0 A_v \dfrac{\partial u}{\partial z} = \tau_{zx}, \;\;\; \rho_0 A_v \dfrac{\partial v}{\partial z} = 0 \;\;\;\;\;\; {\rm at} \; z=0. \]

    • 海面, 海底における熱的条件: 断熱

      \[ \rho_0 K_v \dfrac{\partial \theta}{\partial z} = 0, \;\;\; \rho_0 K_v \dfrac{\partial \theta}{\partial z} = 0 \;\;\;\;\;\; {\rm at} \; z=0, -H. \]

      ここで, \(\theta\) は温位である.

    • 海面における淡水フラックス: なし
  4. 初期条件
    • 運動場: 静止状態
    • 温位の摂動場: 摂動なし
    • 塩分は空間一様を仮定
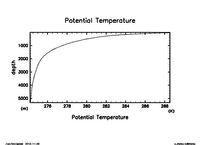
  5. 基本成層場
    • 温位の気候値データの水平平均を与える.
    表1: 海面応力(τzx) および温位の基本場の分布.
    windStressLon_thumb.png z_PTempBasic_thumb.png

3.2 各ケース設定

表2: Kh:水平渦拡散係数[m2 s-1].
実験名 解像度　 Kh
Kh800T42L20 (標準実験) T42L20 8.0 × 102
Kh800T21L20 T21L20 8.0 × 102
Kh800T42L60 T42L60 8.0 × 102
Kh400T42L20 T42L20 4.0 × 102
Kh1600T42L20 T42L20 1.6 × 103
  • ケース Kh800T42L20 は, 鉛直解像度および水平渦拡散係数の依存性を調べるための標準実験である.
    • 水平渦拡散係数 \(K_h=800\) [m2 s-1] の値は, [3], [2] において使われた 等密度面混合[1]の輸送係数を用いる1.
  • 水平解像度の依存性: Kh800T42L20 と Kh800T21L20 の計算結果を比較
  • 鉛直解像度の依存性: Kh800T42L20 と Kh800T42L60 の計算結果を比較
  • 水平渦粘性係数の依存性: Kh400T42L20, Kh800T42L20, Kh1600T42L20 間の計算結果を比較
  1. 各ケースの設定ファイル

4 計算結果

　

4.1 標準実験

  1. 東西流速, 子午面循環
    表3: 左から順に, 東西流速の海面分布の時間発展([m]) , t=300yr における東西流速([m]), 質量流線関数([m2/s])の子午面分布, 運動エネルギーの全球平均の時間発展[m2/(s*kg)].
    xy_U_SeaSurf_thumb.png yz_U_mplane_thumb.png yz_MassStreamFunc_mplane_thumb.png t_EnergyBudget_thumb.png
    • 東西流
      • その向きや大きさは, 海面応力により決定される.
        • 中緯度:西向き, 低緯度: 東向き.
      • 南北の圧力勾配と地衡流バランスしている.
        • 温位が空間的にほぼ一様となるため, 順圧的な分布をとる.
    • 子午面循環
      • 極-緯度30度, 緯度30度-緯度8度, 緯度8度-緯度5度, 緯度5度-赤道に 4 つの循環セルが生じる.
      • 南北流
        • 内部域では東西流速に比べて非常に小さく, 境界近傍においてエクマン流として存在.
          • 海面近く:　低緯度では極向き, 中高緯度では赤道向き
          • 海底近く:　海面近くの南北流と同程度の大きさで, 向きが逆.
      • 鉛直流
        • 上昇域: 赤道, 低緯度域(緯度8度-緯度12度), 高緯度域(緯度50度-極)で上昇.
          • 特に, 赤道上昇流は他の上昇流よりも 3 倍ほど強い.
        • 下降域: 赤道近傍(緯度5度-緯度8度), 低・中緯度域(緯度12度-緯度50度)で下降.
      • 鉛直方向に対してギブス振動が見受けられる. 鉛直解像度依存性を参照.
    • 運動エネルギー
      • 約 5000 日で極大に達した後, 緩やかに減少し定常状態に向かう.
        • 本実験の積分時間(300 年間)のスケールで, 系はほぼ定常に達する.
  2. 温位
    表4: t=30,100,300yr における温位[K]の子午面分布, 海面での温位[K]の時間発展.
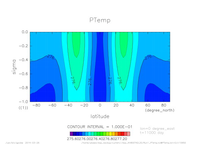
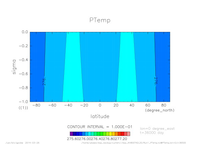
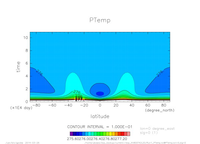
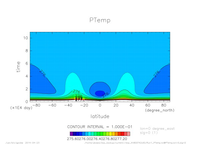
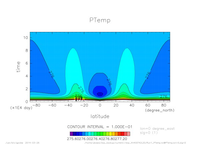
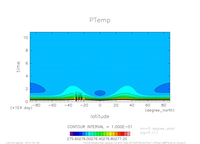
    yz_PTemp_mplane_30yr_thumb.png yz_PTemp_mplane_100yr_thumb.png yz_PTemp_mplane_300yr_thumb.png tz_PTemp_SeaSurf_thumb.png
    • 初期の時間発展(約 30 yr まで)
      • 鉛直拡散により, 初期の基本場の温位の鉛直勾配はすみやかに減少する.
      • 一方, 子午面循環による移流により, 低・高緯度域では相対的に低い下層の温位が上昇, 中緯度の下降域では相対的に高い上層の温位が下降する.
      • 約 100 yr ほどで, 鉛直方向に温位がほぼ一定となる.
    • 運動エネルギーの極大後の時間発展(約 100 yr 後)
      • 残った水平温位勾配は, 子午面循環による移流や水平拡散により, ゆくっりと減少し, 領域全体で温位が一様となる.
  3. 圧力
    表5: t=300yr における圧力偏差(力学的圧力)[Pa] の子午面分布.
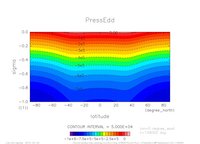
    yz_PressEdd_mplane_thumb.png

4.2 鉛直解像度の依存性(ケース Kh800T42L20(標準実験), Kh800T42L60 の比較)

  1. ケース間での数値解の変化について
    • 海面東西流の比較
      表6: 海面東西流[m]の時間発展(左から順に Kh800T42L20, Kh800T42L60) , 運動エネルギー[m2/(s2*kg)] の全球平均値の時間発展(破線:Kh800T42L20, 実線:Kh800T42L60)の比較. .
      xy_U_SeaSurf_thumb.png xy_U_SeaSurf_thumb.png KEAvg_LCompari_thumb.png
      • Kh800T42L20 の運動エネルギーは, Kh800T42L80 よりも約二倍大きい.
    • 質量流線関数の比較
      表7: t=300 yr の質量流線関数[kg*m2/s]の子午面分布(左から順に Kh800T42L20, Kh800T42L60) の比較. .
      yz_MassStreamFunc_mplane_thumb.png yz_MassStreamFunc_mplane_thumb.png
      • Kh800T42L20 で見られる鉛直方向に対するギブス振動は, 上下端の境界層を解像できる Kh800T42L60 の場合では発生しない.
    • 温位の比較
      表8: t=300yr における温位[K]の子午面分布の比較..
      yz_PTemp_mplane_300yr_thumb.png yz_PTemp_mplane_300yr_thumb.png
      表9: 海面における温位[K]の時間発展の比較..
      tz_PTemp_SeaSurf_thumb.png tz_PTemp_SeaSurf_thumb.png
      • Kh800T42L20 と Kh800T42L60 の間で大きな違いは見られない.

4.3 水平渦拡散・粘性係数の依存性(ケース Kh400T42L20, Kh800T42L20(標準実験), Kh1600T42L20 の比較)

  1. ケース間での数値解の変化について
    • 海面東西流の比較
      表10: 海面東西流[m]の時間発展(左から順に Kh400T42L20, Kh800T42L20, Kh1600T42L20) の比較.
      xy_U_SeaSurf_thumb.png xy_U_SeaSurf_thumb.png xy_U_SeaSurf_thumb.png
      • 水平渦拡散・粘性係数が大きいほど, 赤道の西向きの海面東西流が極大を迎える時期が早く, 極大の値は小さい.
      • 最終状態における海面東西流の違いはほとんどない.
    • 質量流線関数の比較
      表11: t=300 yr の質量流線関数[kg*m2/s]の子午面分布(左から順に Kh400T42L20, Kh800T42L20, Kh1600T42L20) の比較.
      yz_MassStreamFunc_mplane_thumb.png yz_MassStreamFunc_mplane_thumb.png yz_MassStreamFunc_mplane_thumb.png
      • 水平渦拡散・粘性係数による違いは, ほとんど見られない.
    • 温位の比較
      表12: t=300 yr における温位[K]の子午面分布(左から順に Kh400T42L20, Kh800T42L20, Kh1600T42L20) の比較.
      yz_PTemp_mplane_thumb.png yz_PTemp_mplane_thumb.png yz_PTemp_mplane_thumb.png
      表13: 海面における温位[K]の時間発展(左から順に Kh400T42L20, Kh800T42L20, Kh1600T42L20) の比較..
      tz_PTemp_SeaSurf_thumb.png tz_PTemp_SeaSurf_thumb.png tz_PTemp_SeaSurf_thumb.png
      • 水平渦拡散係数が大きいほど, 30 yr 付近の水平温位勾配の大きさが小さく, その後の温位の水平方向の一様化も早い.
  2. 運動エネルギーの収支解析
    • 運動エネルギーの全球平均値の比較
      表14: 運動エネルギーの全球平均値(破線:Kh400T42L20, 実線:Kh800T42L20, 点線:Kh1600T42L20) の比較.
      KEAvg_KhCompari_thumb.png
      • 運動エネルギーのピークを迎える時期は, 水平渦拡散係数が大きいほど早い.
      • 運動エネルギーのピーク時の値は, 水平渦拡散係数が大きいほど 1.5 割程度小さくなるが, 最終状態では大きく変わらない.
    • 運動エネルギーの収支解析とその比較
      表15: 運動エネルギーの全球平均値の収支解析(左から順に Kh400T42L20, Kh800T42L20, Kh1600T42L20) の比較. 各図において, 破線:運動エネルギーの注入率, 実線:正味の変化率, 二点跳び破線:水平渦粘性による散逸, 跳び破線:移流項の仕事, 一点破線:ポテンシャルエネルギーへの変換, 点線:鉛直渦粘性による散逸を表す.
      KEBudget_thumb.png KEBudget_thumb.png KEBudget_thumb.png
      • 約 5000 日で, 海面における運動エネルギーの注入と鉛直渦粘性による散逸がおよそバランスし, 運動エネルギーの成長が止まる.
      • 水平渦拡散・粘性係数が大きいほど, 初期のポテンシャルエネルギーへの変化率は小さい.
      • 水平粘性散逸の寄与は, 運動エネルギーの収支にあまり影響を与えない(ようだ)

5 考察

5.1 各過程がもつ特徴的な時間スケール

  • 子午面循環による移流, 水平渦拡散, 鉛直渦拡散を特徴付ける時間スケールは次のように与えられる.
    • 移流の時間スケール

      H~5 [km], w~2 × 10-6 [m/s] とすれば, Tadvect ~ 2.5 × 104 [days] ~ 70 [yr]

    • 水平拡散の時間スケール

      L~5000 [km], Kh=1× 800 [m2 /s] とすれば, Thdiff ~ 3.0 × 105 [days] ~ 820 [yr]

    • 鉛直拡散の時間スケール

      H~5 [km], Kv=1× 10-2 [m2 /s] とすれば, Tvdiff ~ 2.5 × 104 [days] ~ 70 [yr]

  • Tadvet~Tvdiff << Thdiff の関係にあり, 移流や鉛直拡散の効果が水平拡散より先に現れることが分かる.
  • 運動エネルギーの時間発展におけるピークや温位の水平勾配の極大を迎える時期(約 30 yr後)は, Tadvect, Tvdiff の時間スケールに対応?

5.2 内部領域の東西流の速度スケール

  • 運動エネルギーの収支解析により, 定常状態では海面応力によるエネルギー注入と鉛直渦粘性による散逸がバランスすることが分かる.
  • 定常状態における運動エネルギーのバランスから, 東西流速を見積もることができる.
    • 内部領域では流れはほぼ順圧なので, エネルギー散逸は下側エクマン層(深さ De)で起きとし, 鉛直速度シアの長さスケールを De = 20 [m] でとる.
    • U*τsurface = ρ0 * Av (U/De)2 * D_ e より, U = De * τsurface / (ρ0*Av).
    • 緯度50度の τsurface (=0.12 [kg*m-1*s^1]), ρ0=103 [kg/m3] とすれば, U=0.24 [m/s] となる.
      • 標準実験の内部領域の東西流速と整合的.

6 参考文献

References

[1] Peter R Gent and James C Mcwilliams. Isopycnal mixing in ocean circulation models. Journal of Physical Oceanography, 20(1):150-155, 1990. [ bib ]
[2] John Marshall, David Ferreira, JM Campin, and Daniel Enderton. Mean climate and variability of the atmosphere and ocean on an aquaplanet. Journal of the Atmospheric Sciences, 64(12):4270-4286, 2007. [ bib ]
[3] John Marshall and Timour Radko. Residual-mean solutions for the antarctic circumpolar current and its associated overturning circulation. Journal of Physical Oceanography, 33(11):2341-2354, 2003. [ bib ]
[4] Robin S Smith, Clotilde Dubois, and Jochem Marotzke. Global climate and ocean circulation on an aquaplanet ocean-atmosphere general circulation model. Journal of climate, 19(18):4719-4737, 2006. [ bib ]

脚注:

1

[2] と本計算の混合過程の表現方法は厳密には異なるため, 拡散係数の値を簡単には決定できないが, ここでは安直に同じ値をとることにした.

著者: Kawai Yuta

Created: 2014-04-22 火 21:16

Emacs 23.4.1 (Org mode 8.2.4)

Validate