水惑星設定におけ風成循環の数値実験

2.1 ケース間で共通な設定

1. 計算領域
   
   • 全球的に広がる水深 5.3 km の海洋. 海底地形や陸は存在しない.
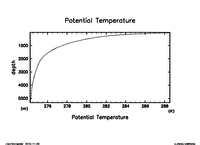
2. 基本成層場
   

   温位の気候値データの水平平均を与える.

3. 散逸
   
   • 水平渦粘性係数

     次の各ケース設定を参照.

   • 鉛直渦粘性係数

     海面の流速が Marshall, et al. (2007) と同程度になるように, \(A_v=1.0 \times 10^{-2}\) [m² s^-1] にとる.

4. 海水の状態方程式
   
   • 線形(Vallis, 2006)
5. 初期条件
   
   • 運動場: 静止状態
   • 温位の摂動場: 摂動なし
   • 塩分は空間一様を仮定
6. 境界条件
   
   • 海面応力

     Marshall, et al. (2007) における準平衡状態での地表風速から計算された, 海面応力の東西平均場を与える.

   • 海面, 海底における熱的条件: 断熱
   • 海面における淡水フラックス: なし

   表1: 海面応力および温位の基本場の分布.

2.2 各ケース設定

3.1 標準実験

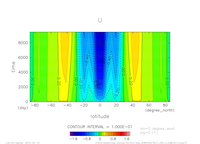
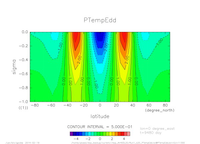
1. 東西流速, 子午面循環
   

   表3: 左から順に, 東西流速の海面分布の時間発展([m]) , t=25yr における東西流速([m]), 質量流線関数([m²/s])の子午面分布, 運動エネルギーの全球平均の時間発展[m²/(s*kg)].

   • 東西流
     • 海面応力と同じ方向の流れ. 中緯度:西向き, 低緯度: 東向き.
     • 東西流速の大きさの順圧的な成分は海面応力によって決定される.
     • 東西流速の傾圧的な成分は, 南北方向の温度勾配を反映している(温度風平衡).
   • 子午面循環
     • 境界近傍のエクマン層によって, 低緯度, 中緯度に 2 つの循環セルが生じる.
       • 南北流
         • 海面近く:　低緯度では極向き, 中高緯度では赤道向き
         • 海底近く:　海面近くの南北流と同程度の大きさで, 向きが逆.
       • 鉛直流: 赤道帯/高緯度域で上昇, 中緯度域で下降する.
     • 内部域では南北流は東西流速と比べ非常に小さい.

   　- 鉛直方向に対してギブス振動が見受けられる. 鉛直解像度依存性を参照.

   • 運動エネルギー
     • この時間積分の時間スケール(25 年間)では, 系は定常に達さない.
2. 温位(偏差)
   

   表4: t=25yr における温位偏差([K]) の子午面分布.

   • 鉛直流の南北分布を反映し, 温度偏差は赤道帯の上昇域では負, 中緯度の下降域では正である.
3. 圧力
   

   hogehoge

3.2 鉛直解像度の依存性(ケース Ah800L20, Ah800L60 の結果の比較)

1. ケース間での数値解の変化について
   
   • 海面東西流の比較

     表5: 海面東西流[m]の時間発展(左から順に Ah800L20, Ah800L60) , 運動エネルギー[m²/(s²*kg)] の全球平均値の時間発展(破線:Ah800L20, 実線:Ah800L60)の比較. .

   • 質量流線関数の比較

     表6: t=25 yr の質量流線関数[kg*m²/s]の子午面分布(左から順に Ah800L20, Ah800L60) の比較. .

   • 温度偏差の比較

     表7: t=25yr における温位偏差[K]の子午面分布の比較..

2. ギブス振動について
   
   • hogehoge

3.3 水平渦粘性係数の依存性(ケース Ah400L20, Ah800L20, Ah1600L20 間の比較)

1. ケース間での数値解の変化について
   
   • 海面東西流の比較

     表8: 海面東西流[m]の時間発展(左から順に Ah400L20, Ah800L20, Ah1600L20) の比較.

   • 質量流線関数の比較

     表9: t=25 yr の質量流線関数[kg*m²/s]の子午面分布(左から順に Ah400L20, Ah800L20, Ah1600L20) の比較.

   • 温度偏差の比較

     表10: t=25yr における温位偏差[K]の子午面分布(左から順に Ah400L20, Ah800L20, Ah1600L20) の比較.

2. 運動エネルギーの収支解析
   
   • 運動エネルギーの全球平均値の比較

     表11: 運動エネルギーの全球平均値(実線:Ah400L20, 破線:Ah800L20, 点線:Ah1600L20) の比較.

   • 運動エネルギーの収支解析とその比較

     表12: 運動エネルギーの全球平均値の収支解析(左から順に Ah400L20, Ah800L20, Ah1600L20) の比較. 各図における線は, 上から順に運動エネルギーの注入率, 移流項の仕事, 正味の変化率, 水平拡散による散逸, ポテンシャルエネルギーへの変換, 鉛直拡散による散逸を表す.