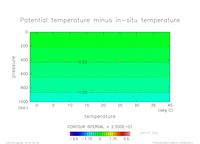
温位と現場温度の差のグラフ
目次
1 海水の温位の定義と特徴
- 流体粒子を圧縮あるいは膨張するとき, 断熱過程においてもその温度は変化する. 温位を導入する目的は, この圧力による効果を考慮することである.
- 海水の温位 \(\theta\) は, [Fofonoff](FM83) において,
\[ \theta (S,T,p) = T + \int_p^{p_r} \Gamma (S,T,p^\prime) \; dp^\prime \]
と定義される. ここで, \(S, T, p, p_r\) はそれぞれ塩分, 温度, 圧力, 参照圧力. また, \(\Gamma = (\partial T/\partial p)_{\rm adiabatic}\) は断熱温度勾配である. \(p_r\) の値には, よくゼロがとられる.
- この \(\theta\) の物理的意味は, \((S,T,p)\) の状態にある流体粒子を, \(S\) を一定に保ちながら断熱的に, \(p\) から \(p_r\) まで移動させたときに得られる 流体粒子の温度である.
- 海洋の典型的な断熱温度勾配の値は, およそ \(0.1 \sim 0.2\) [deg C/km] であるので, 海底(\(5 \sim 10\) [km])における温位と温度の差は 1 度程度.
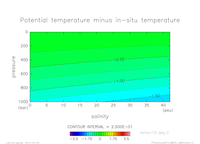
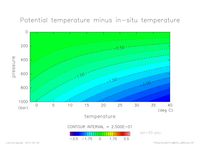
2 温位と現場温度の差のグラフ
以下のグラフでは, いくつかの式から求めた温位と現場温度の差を示す.
2.1 FM83 から求めた温位と現場温度の差グラフ
- 温位は, FM83 の p.42-43 の式群から求める.
- 圧力固定(横軸: 塩分, 縦軸: 温度)
- 温度固定(横軸: 塩分, 縦軸: 圧力)
- 塩分固定(横軸: 温度, 縦軸: 圧力)
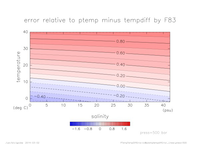
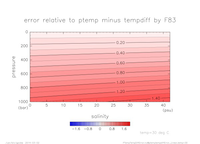
2.2 線形の状態方程式と同じ近似レベルの温位と現場温度の差のグラフ
- 温位は, [Vallis] の (1.154c) から求める.
- FM83 の温位-温度との絶対誤差の二乗平均平方根は, 0.60 [degC].
- 圧力固定(横軸: 塩分, 縦軸: 温度)
- 温度固定(横軸: 塩分, 縦軸: 圧力)
- 塩分固定(横軸: 温度, 縦軸: 圧力)
3 参考文献, 参考リンク
References
| [de Szoeke(2004)] | R. A. de Szoeke. An effect of the thermobaric nonlinearity of the equation of state: A mechanism for sustaining solitary rossby waves. Journal of physical oceanography, 340 (9), 2004. [ bib ] |
| [Fofonoff and Millard(1983)] | N. P. Fofonoff and R. C. Millard. Algorithms for computation of fundamental properties of seawater. 1983. [ bib ] |
| [Vallis(2006)] | G. K. Vallis. Atmospheric and oceanic fluid dynamics: fundamentals and large-scale circulation. Cambridge University Press, 2006. [ bib ] |