風成循環計算における ChebyShev 多項式展開についての考察
目次
1 はじめに
現在開発中の海洋モデルの定式化では, 物理場の鉛直方向の変化は Chebychev 多項式を使った 関数展開によって表現される [Glatzmaier][Boyd]. しかし, 風成循環のテスト計算で見られるように, 鉛直格子点数が足りず海面や海底近傍の境界層を解像できない場合には, 明瞭なギブス振動が内部領域の物理場に現れる.
このギブス振動の対処方法としては, 安直には鉛直格子点数を増やせばよい. 実際, 境界層に対して十分な鉛直解像度の計算において, ギブス振動は消失する.
高解像度計算と標準解像度計算の結果を比較するとき, この風成循環の計算においては, このギブス振動は最低次の循環パターンに重大な影響を与えないことが見て取れる. しかしながら, 物理過程の導入や(場が急激に鉛直方向に変化する)他の物理現象の計算のために, このギブス振動が発生する条件やその特性について考察することは有用だと思われるので, 以下にまとめることにする.
2 検証方法について
以下で与えられる解析的な関数を使って, Chebyshev 多項式展開による数値積分の誤差の収束性を調べる.
2.1 関数の定義
- ケース 1
\(-1 \le \sigma \le 0\) の範囲で連続的に変化する関数
\[ f_1(\sigma) = \sin(k\sigma) \]
を使って, Chebyshev 多項式展開による数値積分の精度を検証する. ここで, \(k\) はモード番号であり, \(k=1,2,3,4,5,6,7,8\) を与える.
- ケース 2
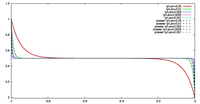
\(-1 \le \sigma \le 0\) の範囲で定義され, 境界付近で急激に値が変化する関数
\[ f_2(\sigma) = \exp{(\dfrac{\sigma}{l_b})} + \exp{ (\dfrac{\sigma-1}{l_b}) } \]
を用いる. ここで, \(l_b\) は境界近傍のおける変化の特徴的な長さスケールであり, \(l_b=0.05,0.01,0.005,0.0025,0.001\) を与える.
この関数形は, 風成循環のテスト計算におけるエクマン層内での急激な場の変化を想定している. その際, 海洋の深さに対するエクマン層の厚さの比は 0.0025 であり, このケースに対しては \(l_b=0.0025\) の場合が対応する.
2.2 数値積分の誤差の評価方法
誤差の評価は, 次に定義される誤差ノルムを指標にして行う.
\[ {\rm ErrorNorm } [ f(\sigma) ] = \dfrac{ \sqrt{ \left( {\rm NumInt}[ f(\sigma) ]_\sigma^0 - {\rm Int}[f(\sigma)]_\sigma^0 \right)^2 }} { {\rm Max} \left[ {\rm Int}[f(\sigma)_{\sigma}^0 ] \right] } \]
ここで, \({\rm NumInt}[\;]_\sigma^0\) は \([\sigma, 0]\) 間の数値積分による定積分, \({\rm Int}[\;]_\sigma^0\) は \([\sigma, 0]\) 間の解析的な定積分を表す. また, \({\rm Max}[\;]\) は区間内での最大値を示す.
2.3 解像度の設定
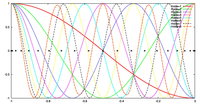
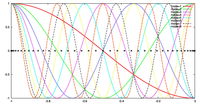
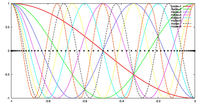
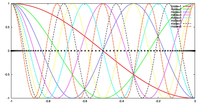
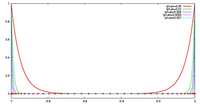
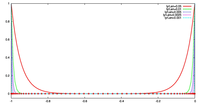
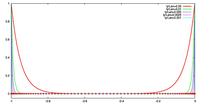
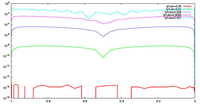
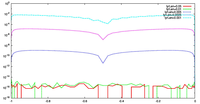
ケース 1, 2 の両方において, 格子点数を 20, 40, 60, 80 に変化させて, 誤差の収束性を議論する. 場が変化する場所と格子点の配置の対応を表す図は, 検証結果において示す.
3 検証結果
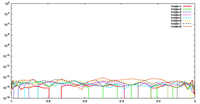
3.1 ケース 1 : 連続的に場が変化する場合
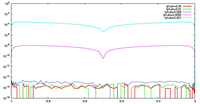
- 場の分布および格子点の配置
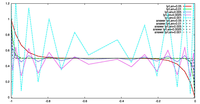
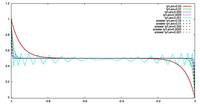
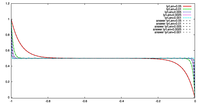
- 数値誤差の収束性
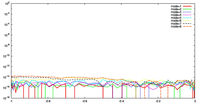
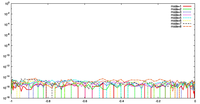
3.2 ケース 2 : 境界近傍で急激に場が変化する場合
- 場の分布および格子点の配置
- 数値誤差の収束性
- 数値積分により得られた値の分布の特徴
4 参考文献, 参考リンク
References
| [Boyd(1999)] | J. P. Boyd. Chebyshev and fourier spectral methods. 1999. [ bib ] |
| [Glatzmaier(1984)] | G. A. Glatzmaier. Numerical simulations of stellar convective dynamos. i. the model and method. Journal of Computational Physics, 550 (3):0 461-484, 1984. [ bib ] |