<< z 方向の温位の移流 (クーラン数固定, タイムフィルタあり) >>

z 方向に温位の擾乱が移流する様子を計算する. 
4 次精度中心差分演算ルーチンを用いる. 
ここではクーラン数が 0.5 程度になるように固定して時間ステップ/空間解像度を変えて 3 通り計算する.
プログラムソース arare2
基本場の温度 温度一様(298.15 K)
音速 347 m/s
z 方向の風速 35 m/s
音波の減衰 なし
粘性 なし
重力 なし
定圧比熱 1004 J K^-1 kg^-1
積分時間 300 秒
計算領域 水平(x) : 10000 m
鉛直(z) : 10000 m
境界条件 水平(x) : 周期境界条件
鉛直(z) : 周期境界条件
数値解法 水平(x) : 陽解法
鉛直(z) : 陰解法
アッセリンの時間フィルタの係数 0.1 

なお, 音波関連項の計算は行っていない. 
そうしないと z 方向に対して周期境界条件を設定すると計算が崩壊してしまう.

[HOME]
 
4 次精度中心差分演算ルーチンを用いた結果
空間解像度 50
時間ステップ 1.5 s
クーラン数 0.26
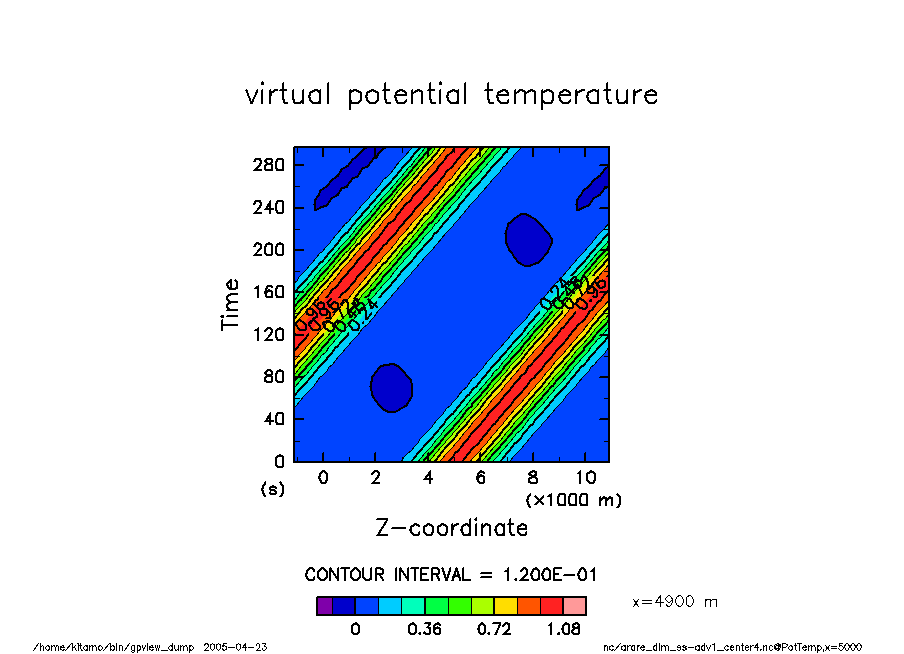
arare_dim_ss-adv1_center4
温位擾乱の時間変化
arare_dim_ss-adv1_center4-t0
温移擾乱(t = 0)

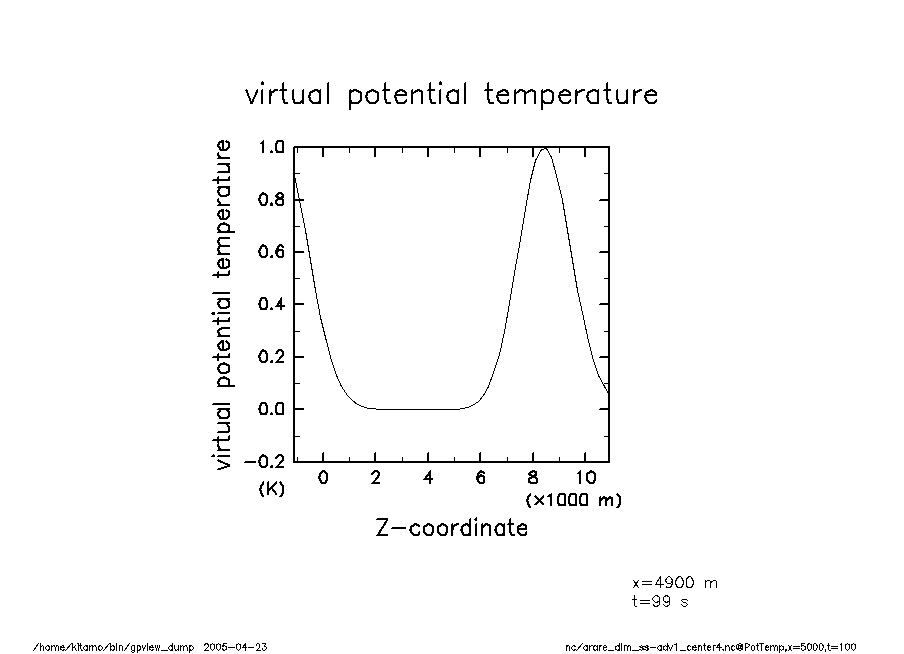
arare_dim_ss-adv1_center4-t100
温移擾乱(t = 100)
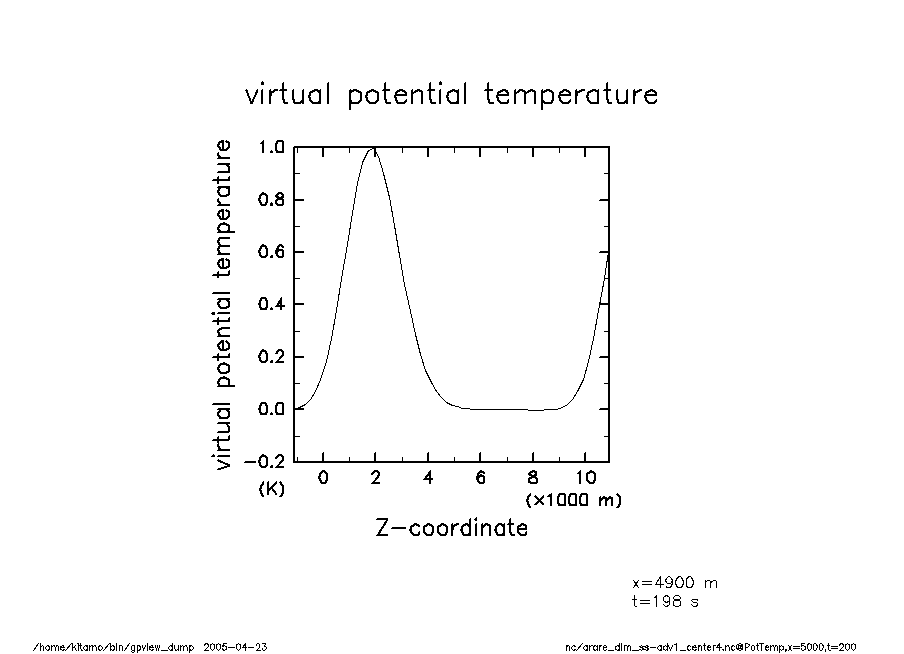
arare_dim_ss-adv1_center4-t200
温移擾乱(t = 200)
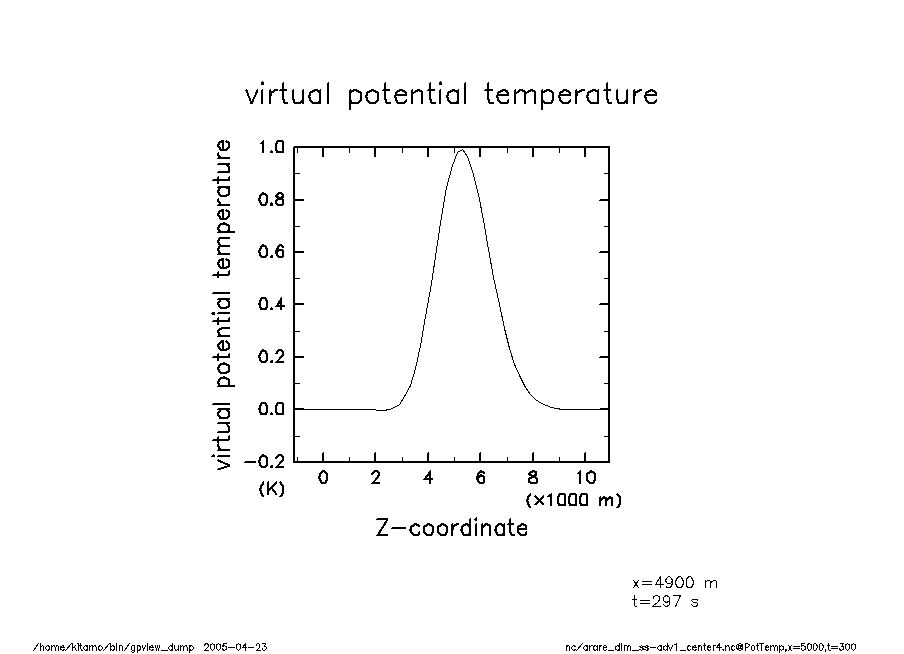
arare_dim_ss-adv1_center4-t300
温移擾乱(t = 300)
空間解像度 50
時間ステップ 3 s
クーラン数 0.53
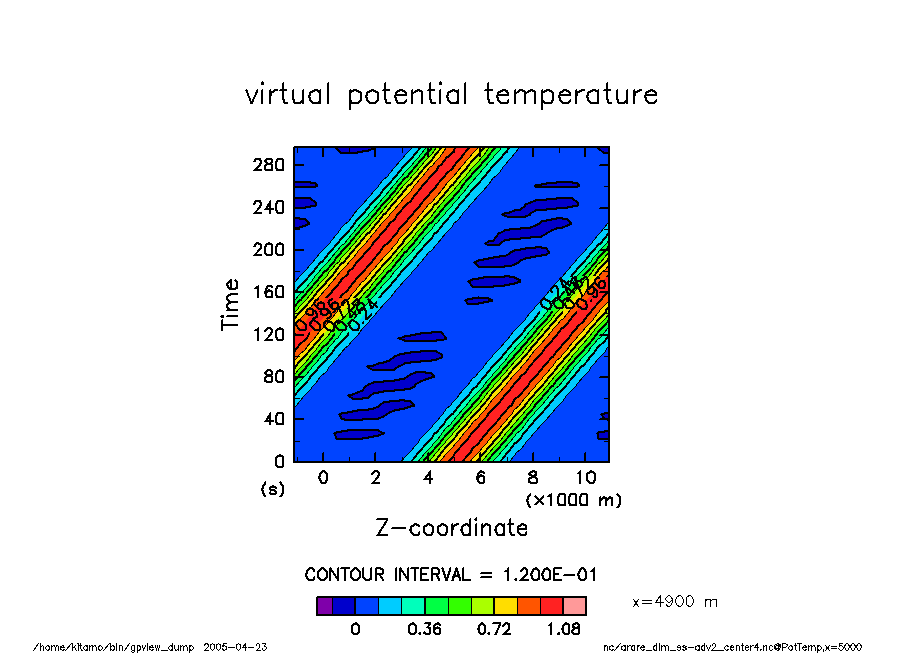
arare_dim_ss-adv2_center4
温位擾乱の時間変化
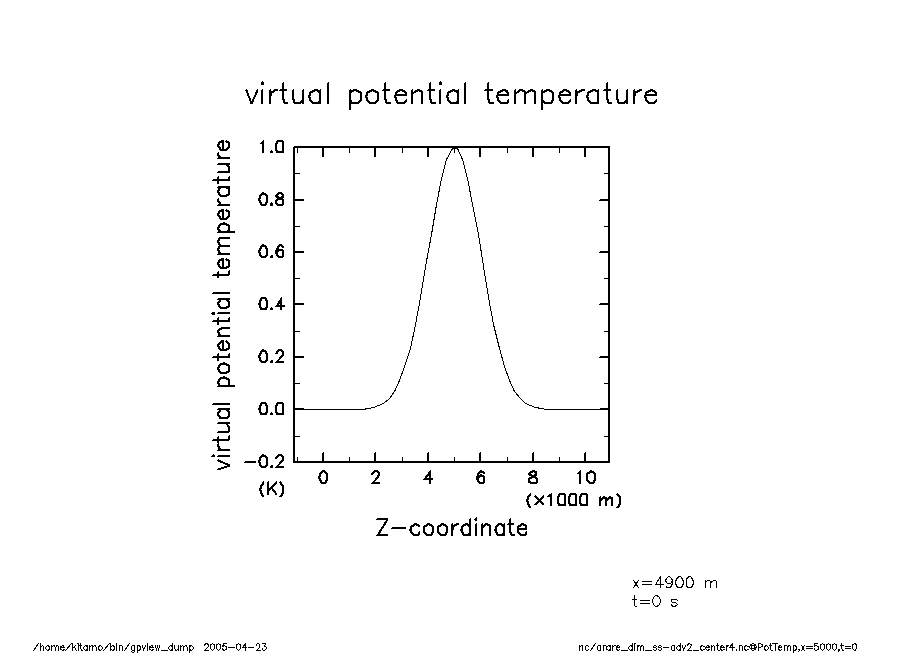
arare_dim_ss-adv2_center4-t0
温移擾乱(t = 0)

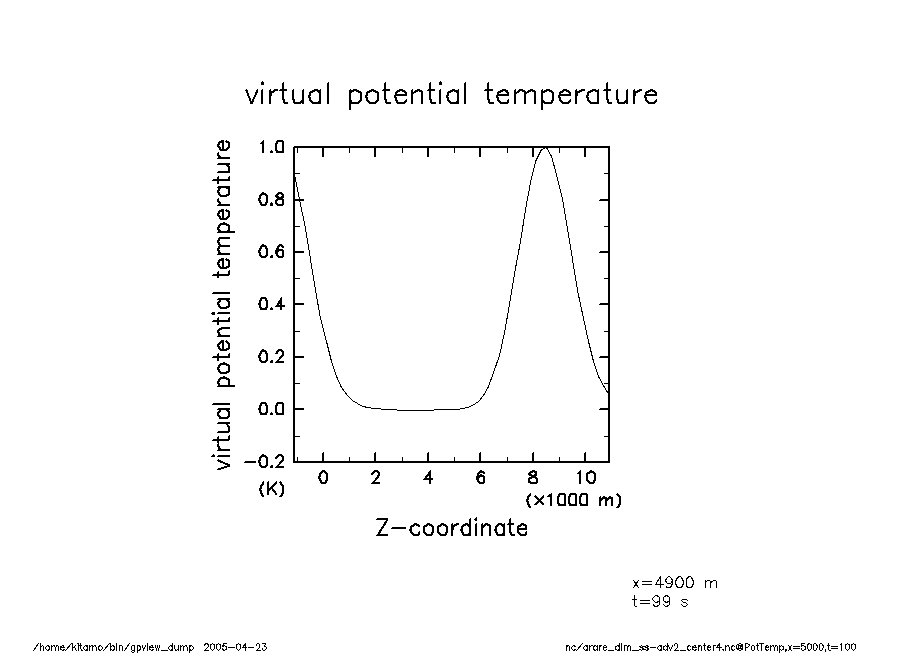
arare_dim_ss-adv2_center4-t100
温移擾乱(t = 100)
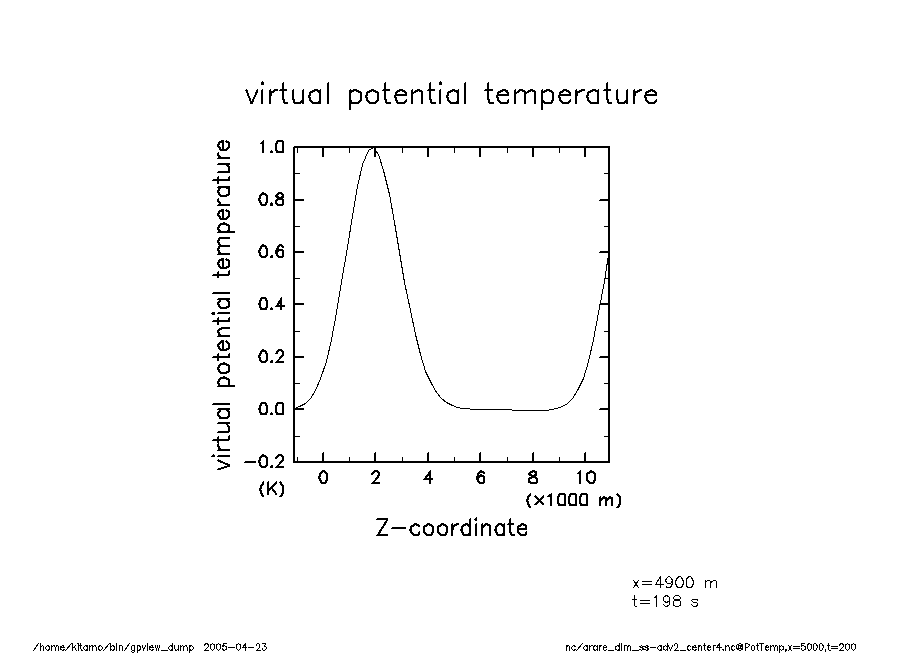
arare_dim_ss-adv2_center4-t200
温移擾乱(t = 200)
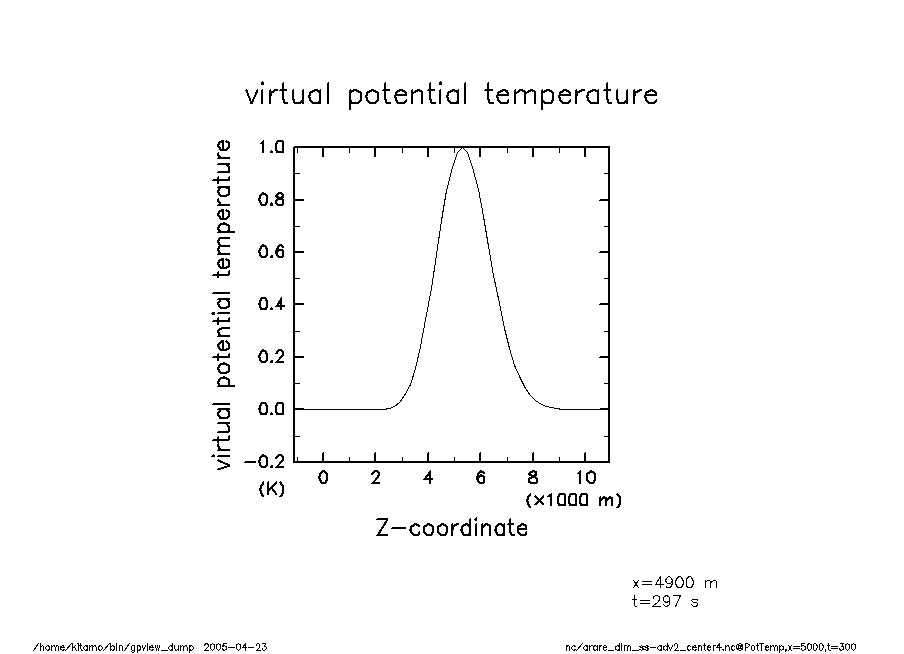
arare_dim_ss-adv2_center4-t300
温移擾乱(t = 300)
空間解像度 50
時間ステップ 4.5 s
クーラン数 0.79
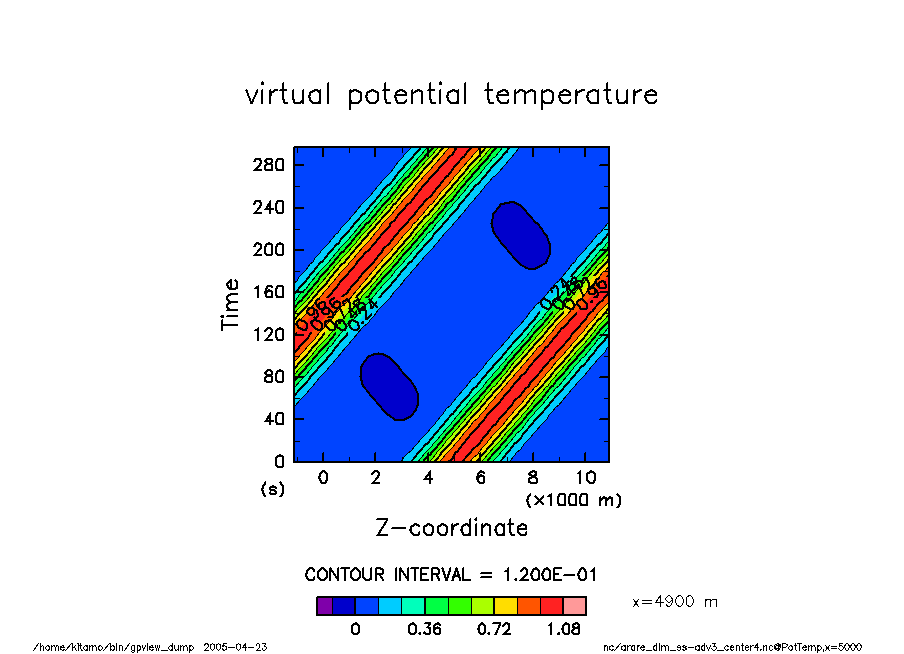
arare_dim_ss-adv3_center4
温位擾乱の時間変化
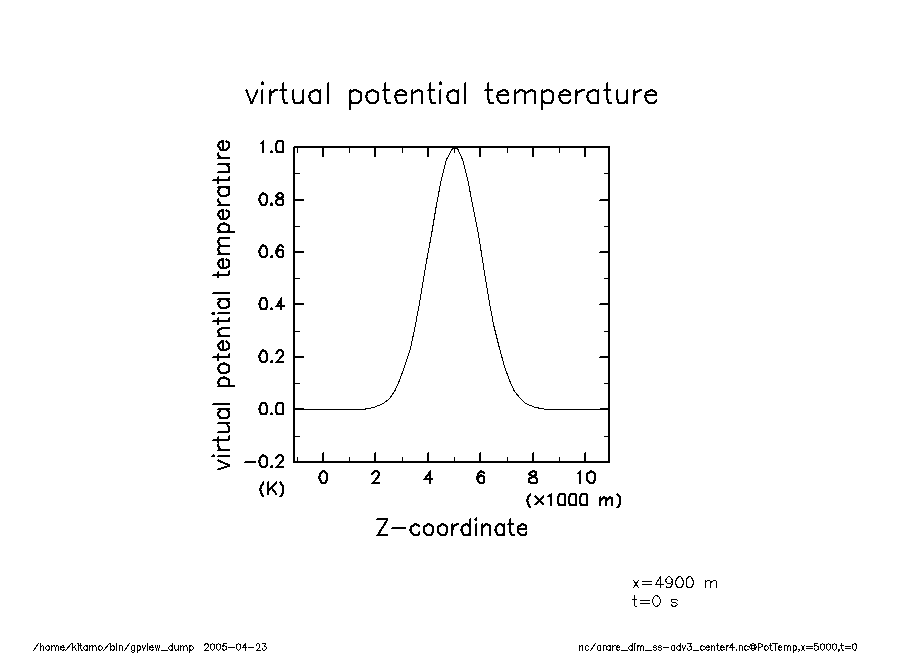
arare_dim_ss-adv3_center4-t0
温移擾乱(t = 0)

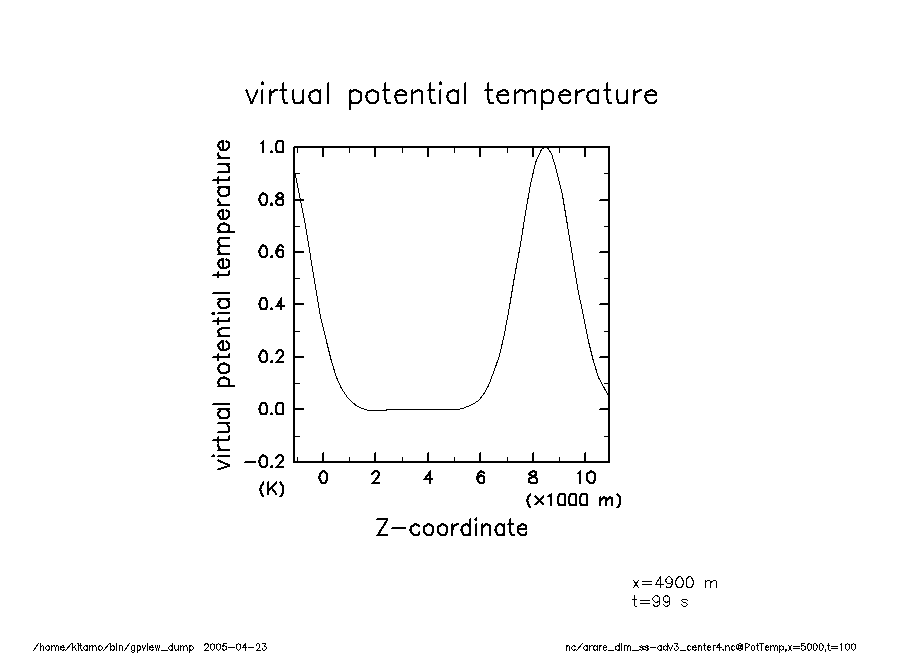
arare_dim_ss-adv3_center4-t100
温移擾乱(t = 100)
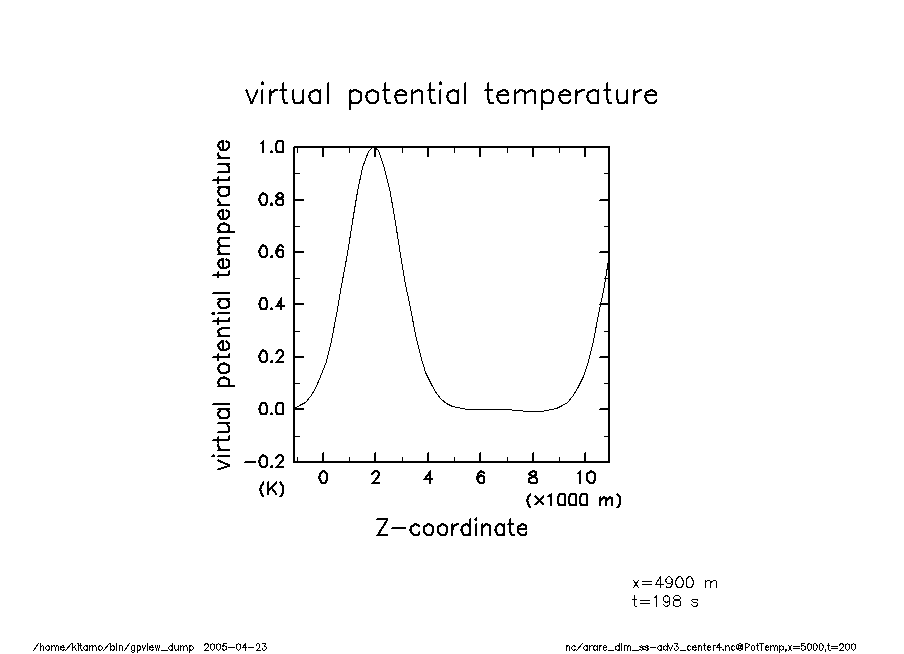
arare_dim_ss-adv3_center4-t200
温移擾乱(t = 200)
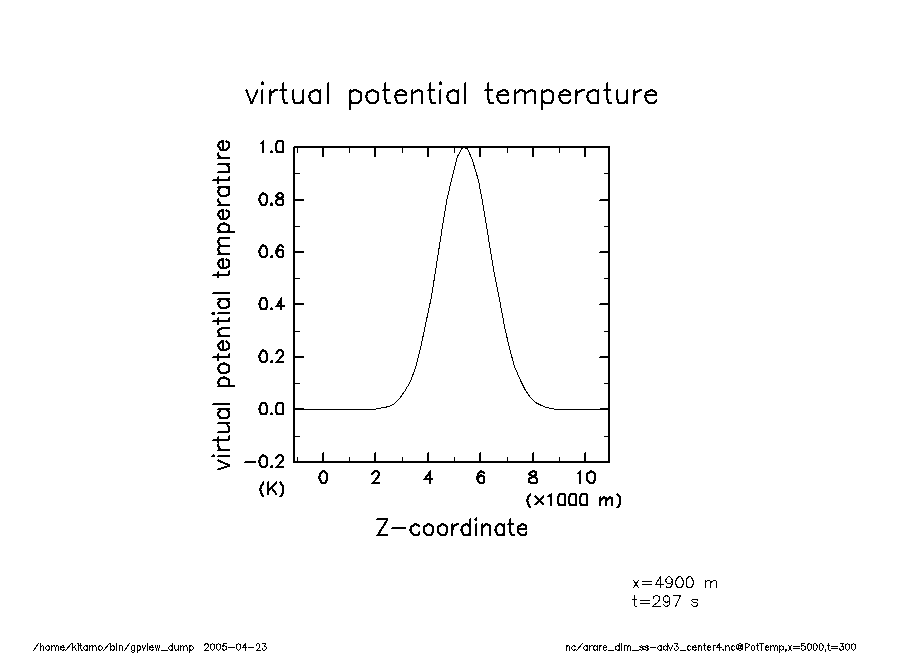
arare_dim_ss-adv3_center4-t300
温移擾乱(t = 300)
2 次精度中心差分演算ルーチンを用いた結果
空間解像度 50
時間ステップ 1.5 s
クーラン数 0.26
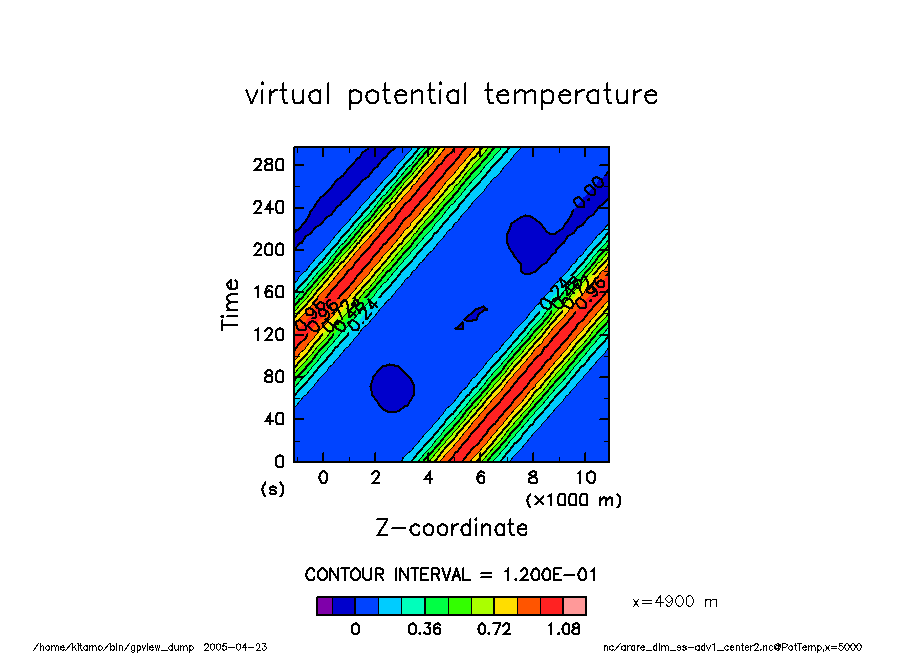
arare_dim_ss-adv1_center2
温位擾乱の時間変化
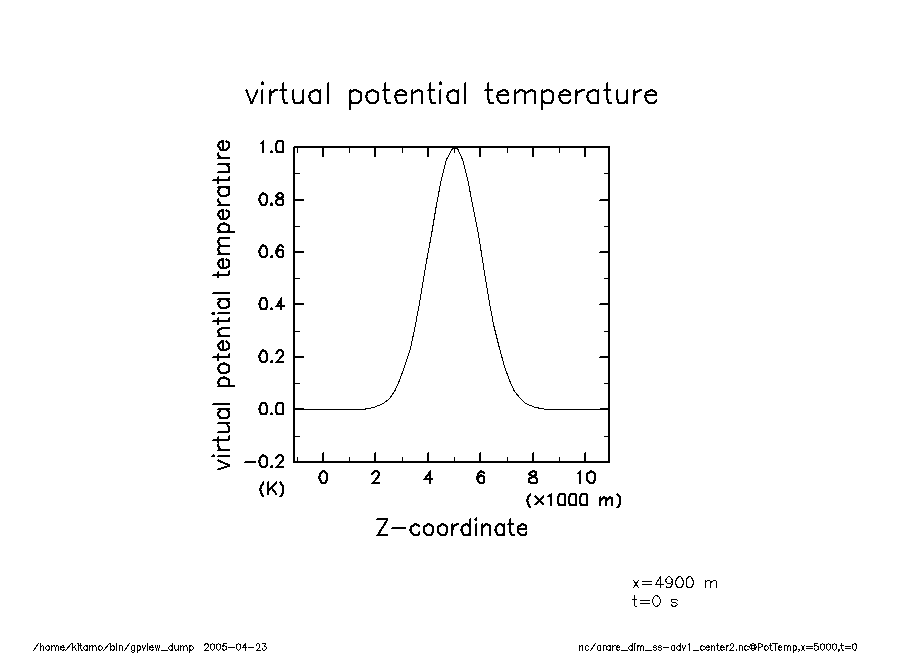
arare_dim_ss-adv1_center2-t0
温移擾乱(t = 0)

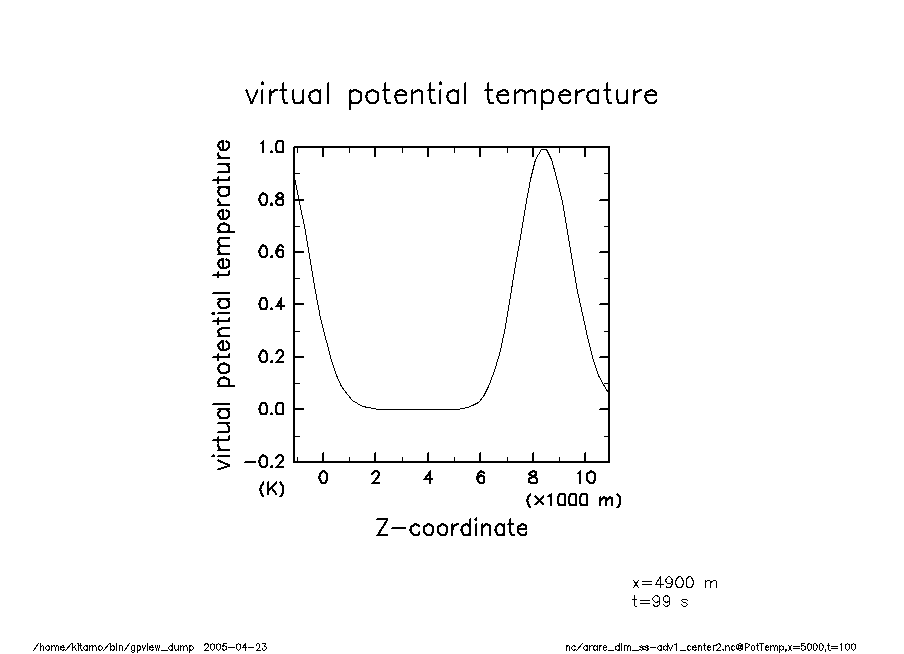
arare_dim_ss-adv1_center2-t100
温移擾乱(t = 100)
arare_dim_ss-adv1_center2-t200
温移擾乱(t = 200)
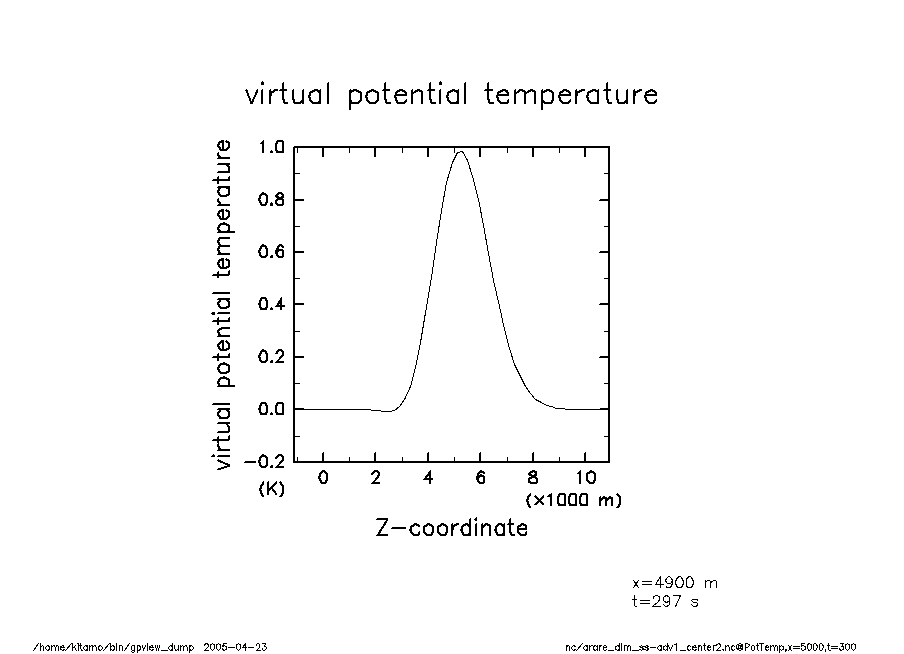
arare_dim_ss-adv1_center2-t300
温移擾乱(t = 300)
空間解像度 50
時間ステップ 3 s
クーラン数 0.53
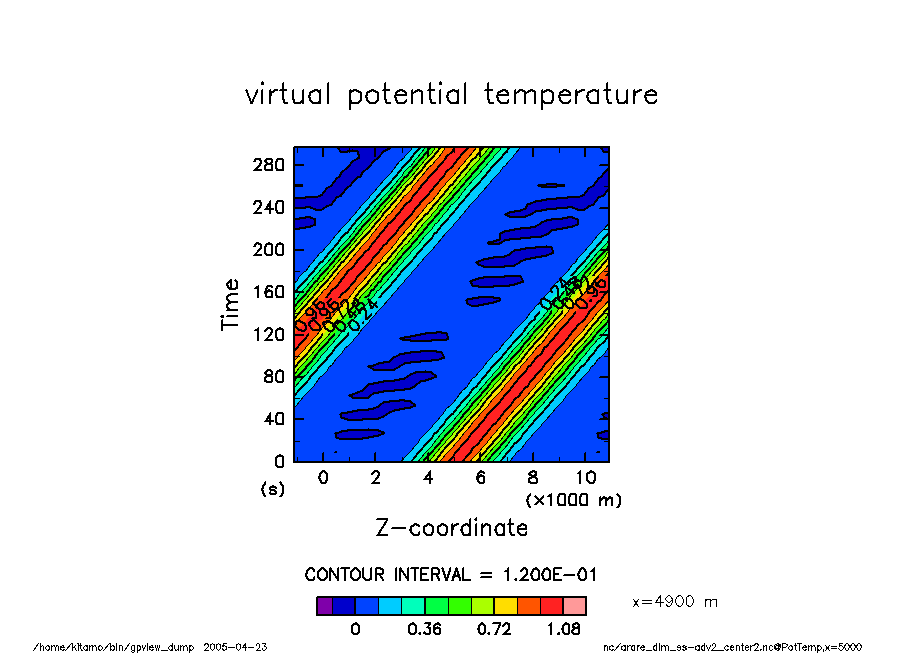
arare_dim_ss-adv2_center2
温位擾乱の時間変化
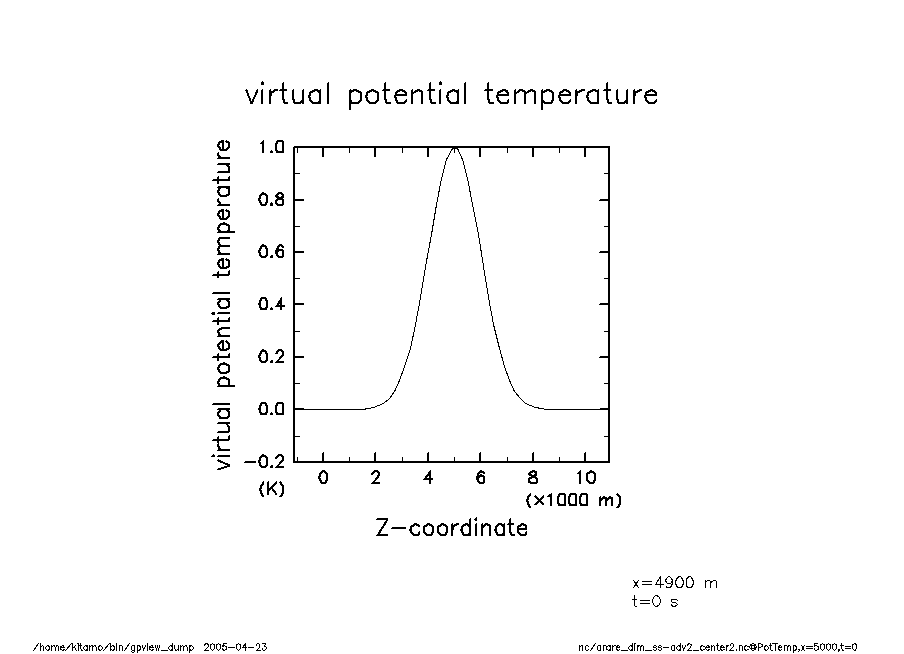
arare_dim_ss-adv2_center2-t0
温移擾乱(t = 0)

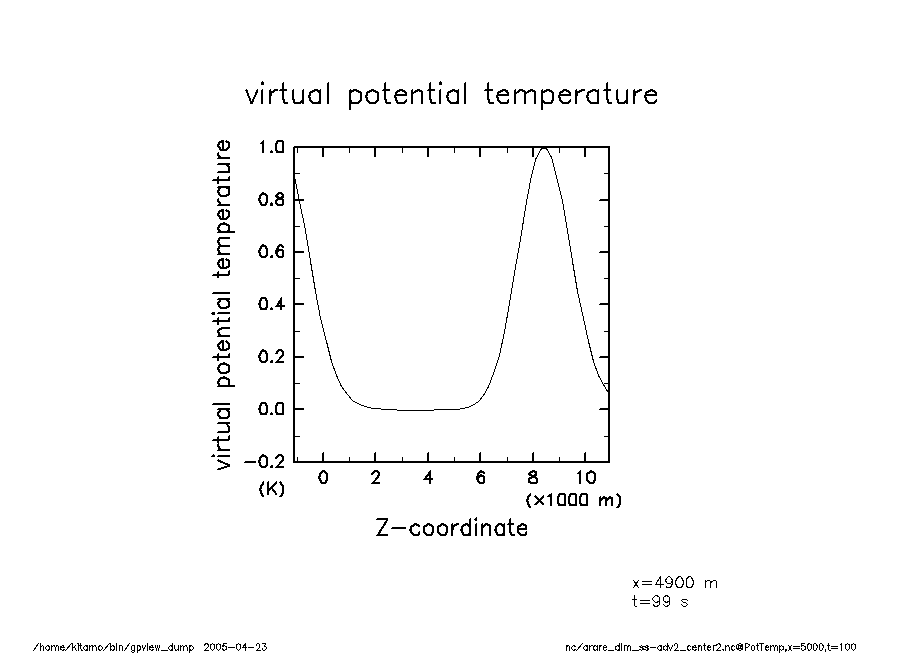
arare_dim_ss-adv2_center2-t100
温移擾乱(t = 100)
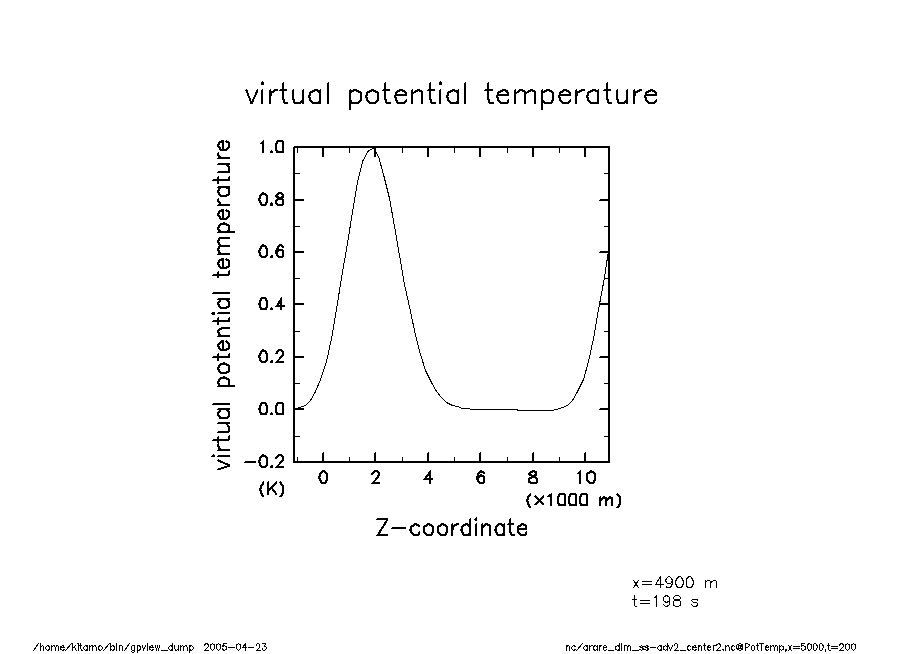
arare_dim_ss-adv2_center2-t200
温移擾乱(t = 200)
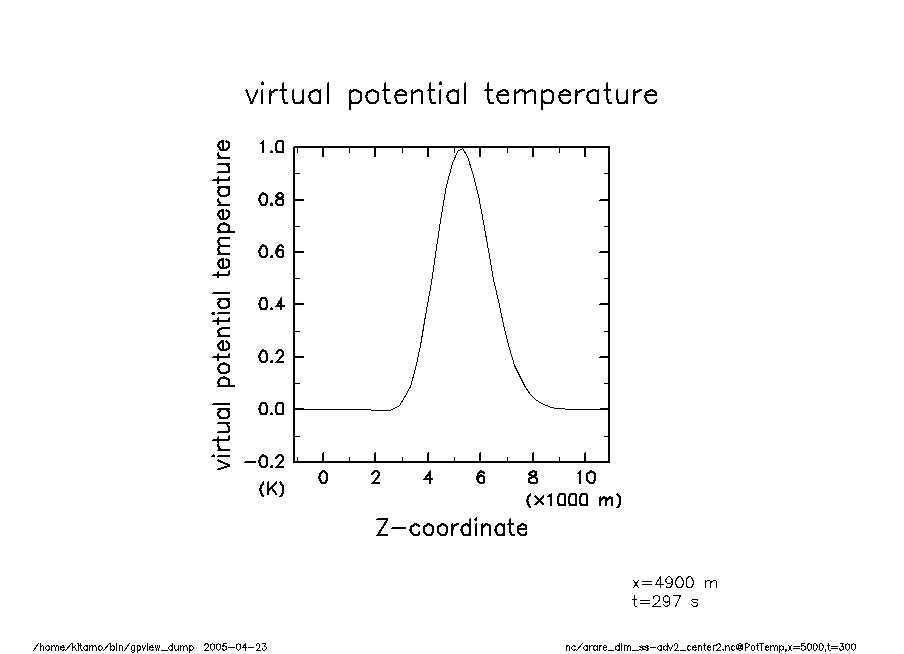
arare_dim_ss-adv2_center2-t300
温移擾乱(t = 300)
空間解像度 50
時間ステップ 4.5 s
クーラン数 0.79
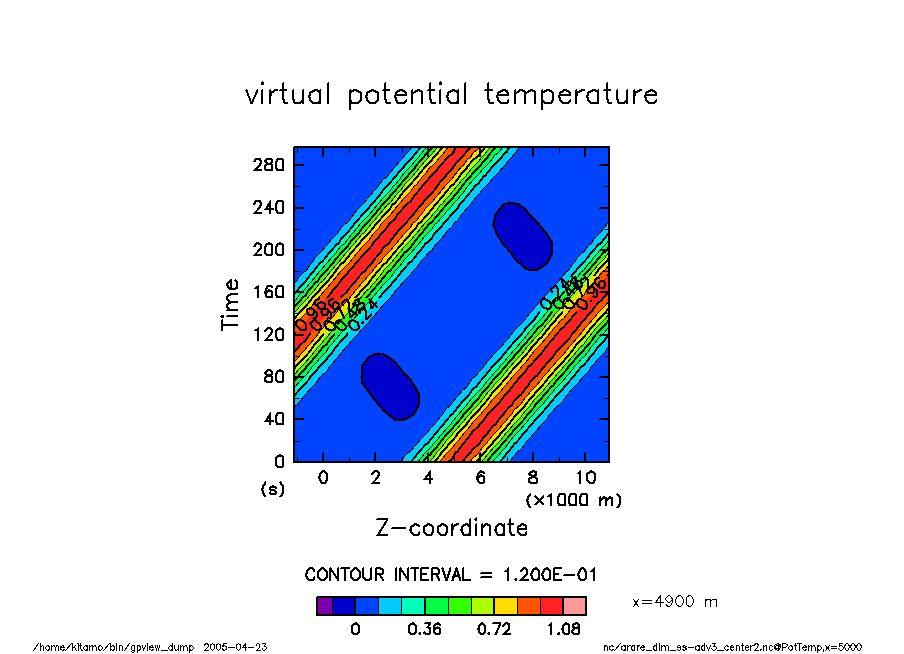
arare_dim_ss-adv3_center2
温位擾乱の時間変化
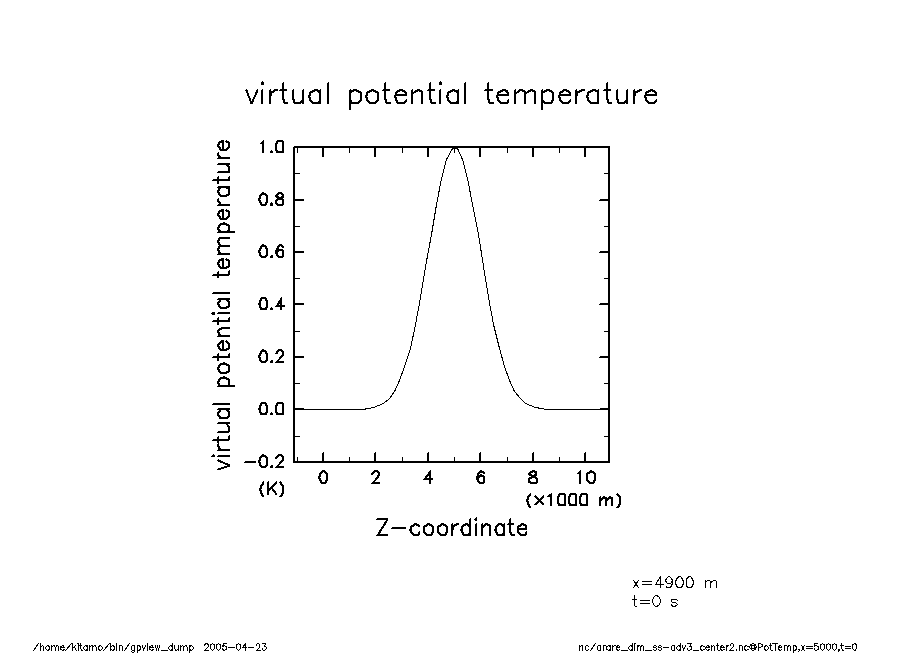
arare_dim_ss-adv3_center2-t0
温移擾乱(t = 0)

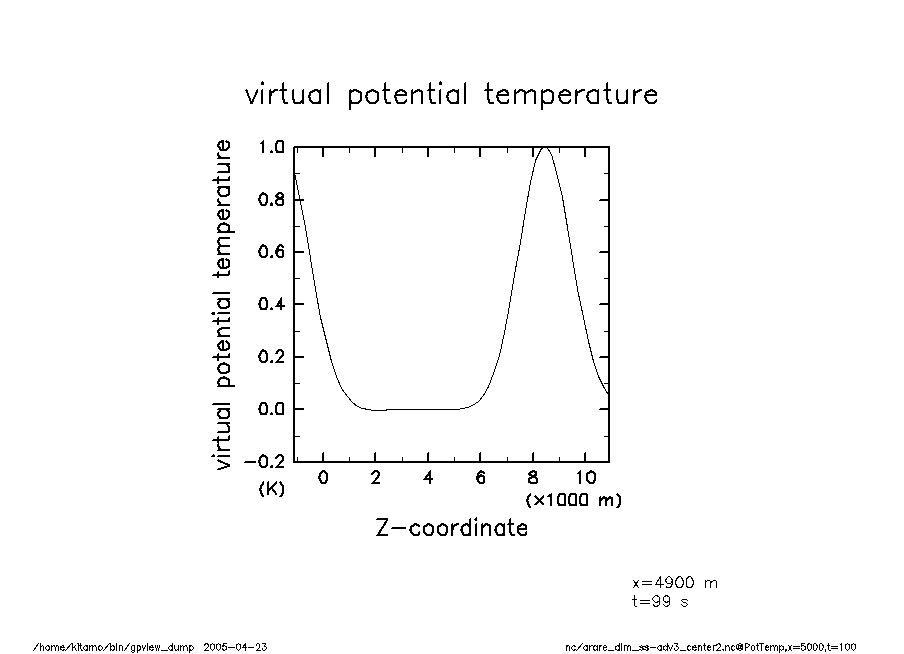
arare_dim_ss-adv3_center2-t100
温移擾乱(t = 100)
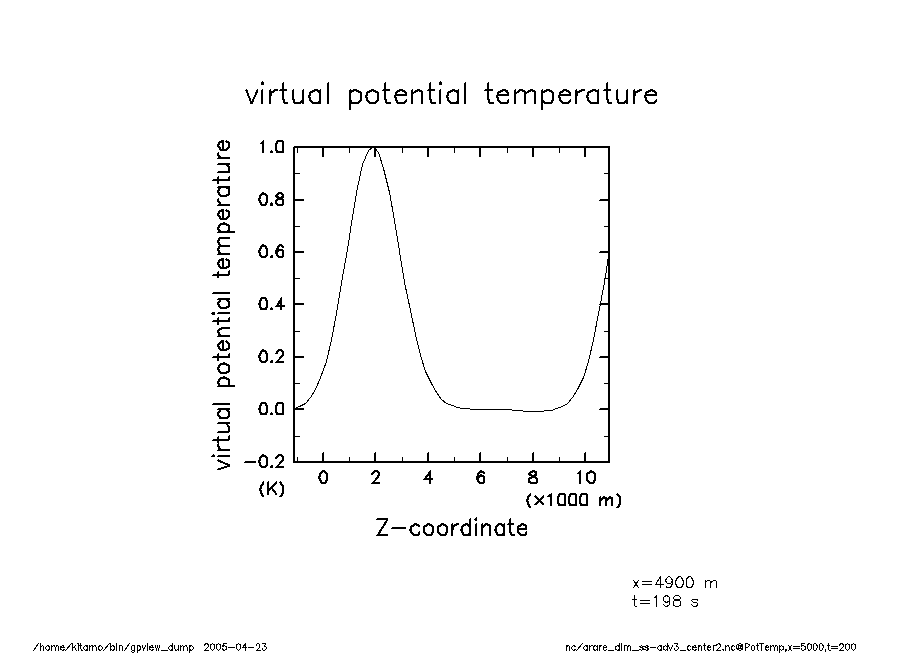
arare_dim_ss-adv3_center2-t200
温移擾乱(t = 200)
arare_dim_ss-adv3_center2-t300
温移擾乱(t = 300)
Last update: Wed Apr 20 19:08:30 JST 2005
Copyright © deepconv 2005 (北守 太一)