/地球流体セミナー
/講演資料一覧
/2003-09-08/
連続モードに隠されたモードの共鳴による不安定
伊賀 啓太(九大・応用力学研究所)
2003 年 9 月 9 日
講演ビデオを見るには, 以下の各スライド画像をクリックし,
左上に表示される「ビデオ開始」をクリックしてください.

|
タイトルぺージ
|

|
問題意識
- 不安定が起こる場合に中立波が見付からないときはどうするか?
|
|
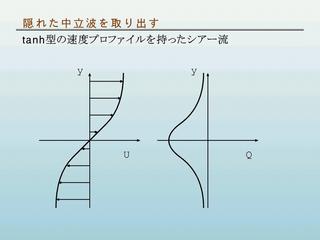
中立波のない例 :
tanh 型の速度分布
|
|
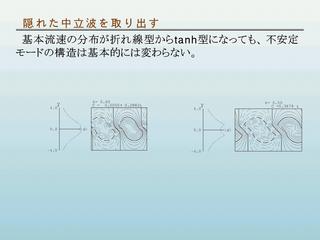
不安定モードの構造
折れ目のある速度分布を持つ場合とよく似た構造を持つ.
|

|
分散曲線
- 正則な波は不安定波だけ.
- k = 1 で不安定波に接続される cr = 0 付近の
2 つの中立波の共鳴 ?
- 数値計算時の格子間隔を細かくするといくらでも cr = 0
に近付いていくので, よろしくない.
|
|
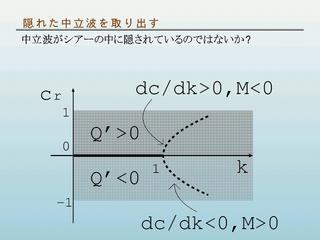
隠れた中立波を取り出す
中立波があると仮定する
- 分散曲線の傾きから, 擬運動量の符号を推定する.
- dc/dk > 0 のとき M < 0
- dc/dk < 0 のとき M > 0
- これらの場合は不安定がどのように起こるかよくわからない.
部分系を考える 2 つの方法
- U = cr でないようにする (シアーをなくす)
- 基本場の Q が一様
|

|
考えている領域の一部だけ部分系をあてはめる.
|

|
tanh 型速度分布に適用した例
|

|
「窓」を開けた場合の分散関係
- 隠れた中立波の一部が見えると思ったのだか…
- 中立波の分散曲線ではないらしい (次のスライド参照)
|
|
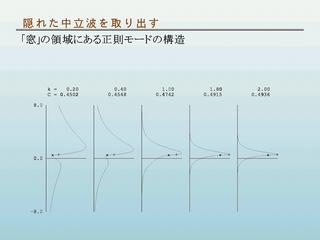
「窓」領域の正則なモードの y 方向の構造
- × 印は y = y1, + 印は y = y2
を表す.
|

|
「窓」のどの点を取り出すか?
- 窓の境界付近は Q の不連続の影響が大きい
- 窓の中央の点をとることにする.
|

|
「窓」の中央の点を選択する意味は ?
- Rayleigh 方程式を「窓」の境界を挟む領域で積分する.
|

|
関数の 1 階微分の飛びとの対応
- 窓の中央で飛びを打ち消し合う
- 飛びを打ち消し合う場所が隠れた中立波に対応するのはなぜ?
|

|
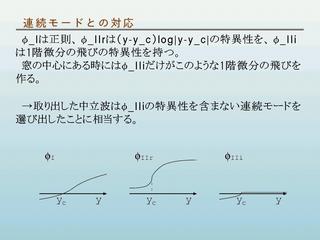
連続モードとの対応
- 連続モードの基本解は 3 つ
- どの基本解 or その組合せに対応する解を取り出したことになっているか ?
|
|
連続モードとの対応
- 「窓」の中央に対応するモードは,
連続モードの一部を取り除いたものに対応する.
- 1 階微分の特性を持たない連続モードの和で表される.
|

|
分散関係
- 紫 : 「窓」を開けて調べた点
- 赤 : 固有関数から推定した点
|
|
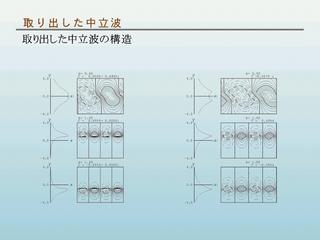
中立波の構造
- 左 : tanh 型速度分布場合
- 右 : 折れ目のある速度分布の場合
|

|
まとめ
|

|
参考文献 1
|

|
参考文献 2
|

|
参考文献 3
|
|
|
参考文献
- Bretherton, F. P., 1966:
Critical layer instability in baroclinic flows.
Quart. J. Roy. Meteor. Soc.,
92, 325-334.
- Cairns, R. A., 1979:
The role of negative energy waves in some instabilities of parallel flows.
J. Fluid Mech., 92, 1-14.
- Case, K. M., 1960:
Stability of inviscid plane Couette flow.
Phys. Fluids, 3, 143-148.
- Hayashi, Y.-Y. and Young, W. R., 1987:
Stable and unstable shear modes on rotating parallel flows in
shallow water. J. Fluid Mech., 184, 477-504.
- Iga, K., 1993
Reconsideration of Orlanski's instability theory of frontal waves.
J. Fluid Mech., 255,213-236.
- Iga, K., 1997,
Instability of a front with a layer of uniform potential vorticity.
J. Meteor. Soc. Japan, 75, 1-11.
- Iga, K., 1999a:
Critical layer instability as a resonance
between a non-singular mode and continuous modes.
Fluid Dyn. Res., 25, 63-86.
- Iga, K., 1999b,
A simple criterion for the sign of the pseudomomentum
of modes in shallow water systems.
J. Fluid Mech., 387, 343-352.
- Lin, C. C., 1945:
On the stability of two-dimensional parallel flows Part.II.
Quart. Appl. Math., 3, 218-234.
- Lin, C. C., 1961:
Some mathematical problems in the theory of the stability of parallel
flows. J. Fluid Mech., 10, 430-438.
- Orlanski, I., 1968:
Instability of frontal waves. J. Atmos. Sci.,
25, 178-200.
- Sakai, S., 1989:
Rossby-Kelvin instability: a new type of ageostrophic instability
caused by a resonance between Rossby waves and gravity waves.
J. Fluid Mech., 202, 149-176.
- Satomura, T., 1981: An investigation of shear onstability in a shallow water. J. Met. Soc. Japan, 59, 148-167.
|
Odaka Masatsugu
2003-09-09
|