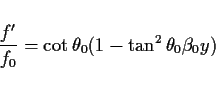![]() は現象の時間スケールと地球が自転する時間スケールとの比を表
す無次元数で, 大洋スケールの現象を扱っている場合には, 一般に時間スケール
が 1 日よりも長いので,
は現象の時間スケールと地球が自転する時間スケールとの比を表
す無次元数で, 大洋スケールの現象を扱っている場合には, 一般に時間スケール
が 1 日よりも長いので,
![]() である. また現象の時間スケー
ルが T=L/U で表される場合には
である. また現象の時間スケー
ルが T=L/U で表される場合には
![]() は
は ![]() と等しくなる.
と等しくなる.
![]() はロスビー数と呼ばれる無次元数で, コリオリ項と移流項の比を表
している. f0 が慣性重力波の伝播する時間スケールであることから, 水平距
離 L を流速 U で動くのに要する時間と慣性重力波が伝播する時間との比を
表しているとも言える. 大洋スケールの現象の場合,
はロスビー数と呼ばれる無次元数で, コリオリ項と移流項の比を表
している. f0 が慣性重力波の伝播する時間スケールであることから, 水平距
離 L を流速 U で動くのに要する時間と慣性重力波が伝播する時間との比を
表しているとも言える. 大洋スケールの現象の場合,
![]() ,
,
![]() であることから,
であることから,
![]() となる. EH, EV はそれぞれ水平エクマン数, 鉛直エ
クマン数と呼ばれる無次元数で, 粘性項がコリオリ項に対してどの程度の大きさ
を持つのかを表している.
となる. EH, EV はそれぞれ水平エクマン数, 鉛直エ
クマン数と呼ばれる無次元数で, 粘性項がコリオリ項に対してどの程度の大きさ
を持つのかを表している.
![]() ,
,
![]() 程度とすると, それぞれ
程度とすると, それぞれ
![]() ,
,
![]() 程度となり, 1 よりはるかに小さいことがわか
る.
程度となり, 1 よりはるかに小さいことがわか
る. ![]() はコリオリパラメータの緯度変化の度合を表す無次元数で,
はコリオリパラメータの緯度変化の度合を表す無次元数で,
![]() 程度である.
程度である.
以上のスケーリングをもとに, (10), (11) 式から O(1)よりもはるかに小さい項を無視すると以下を得る.