|
The monoclomatic optical depth  for wave number
for wave number 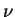 is represented
by using the extinction coefficient per unit volume
is represented
by using the extinction coefficient per unit volume 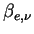 as follows.
as follows.
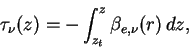 |
(A.39) |
where  is altitude at the top of atmosphere. is altitude at the top of atmosphere.
 is given as follows. is given as follows.
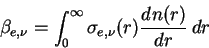 |
(A.40) |
where 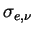 is the extinction cross section, is the extinction cross section,
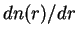 is the size distribution of scattering particle
(cf. Liou, 1980;
Shibata, 1999).
By using extinction coefficient per unit mass is the size distribution of scattering particle
(cf. Liou, 1980;
Shibata, 1999).
By using extinction coefficient per unit mass 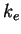 ,
(A.40) is rewritten as follows. ,
(A.40) is rewritten as follows.
 |
(A.41) |
where 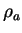 is atmospheric density, and is atmospheric density, and  is
mass mixing ratio of scattering particle.
Similarly, the scattering and absorption coefficient per unit volume
are represented by using the scattering cross section is
mass mixing ratio of scattering particle.
Similarly, the scattering and absorption coefficient per unit volume
are represented by using the scattering cross section 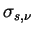 and the absorption cross section and the absorption cross section 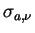 as follows. as follows.
and the single scattering albedo 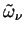 is given as follows. is given as follows.
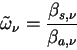 |
(A.44) |
The extinction efficiency 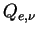 is defined as
the ration of extinction cross section to geometric cross section. is defined as
the ration of extinction cross section to geometric cross section.
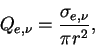 |
(A.45) |
Similarly,
the scattering efficiency 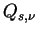 and
absorption efficiency and
absorption efficiency  are defined as follows. are defined as follows.
In present study, the dust opacity is derived from the
mass mixing ratio of atmospheric dust.
Given parameters are the cross section weighted mean extinction
efficiency 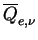 , the single scattering albedo , the single scattering albedo 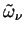 , the size distribution function of dust , the size distribution function of dust
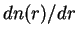 , the effective (or, cross section
weighted mean) radius , the effective (or, cross section
weighted mean) radius 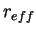 , and the density of dust
particle , and the density of dust
particle 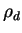 . .
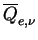 , , 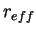 are defined as
follows, respectively. are defined as
follows, respectively.
Supposing that the shape of scattering particle is sphere,
the extinction coefficient per unit mass is given as follows.
where 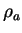 is the atmospheric density.
Therefore, the optical depth can be represented as follows. is the atmospheric density.
Therefore, the optical depth can be represented as follows.
 |
(A.51) |
|