|
付録 A.e 節 に示した
(A.55)
の離散化は時間方向には Clank-Nicolson 法, 空間方向には中心差分を用いて行う.
温度と格子間隔を整数格子点, 熱フラックスを半整数格子点で評価する.
鉛直方向の格子点数は 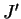 とし, 最下層から とし, 最下層から
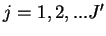 とする. 最上層の温度 とする. 最上層の温度 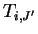 が地表面温度 が地表面温度 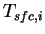 である.
である.
ここで
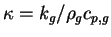 である. 時刻 である. 時刻 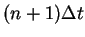 の項を左辺に, 時刻 の項を左辺に, 時刻 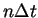 の項を右辺にまとめると, の項を右辺にまとめると,
ここで
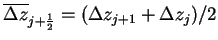 とした. とした.
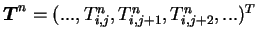 とすると, 行列式の形で とすると, 行列式の形で
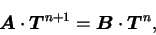 |
(B.61) |
と表すことができる. ここで
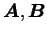 はそれぞれ, はそれぞれ,
を要素に持つ 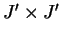 行列である. 行列である.
(A.56)
式で表された上端での境界条件と下端で断熱境界条件を考慮すると,
(B.61) は
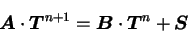 |
(B.62) |
となる. したがって
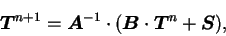 |
(B.63) |
を解くことになる.
ここで係数行列
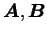 の第 1 行および第 の第 1 行および第 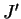 行の対角要素は, 行の対角要素は,
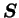 は は 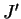 行列ベクトルで, 行列ベクトルで,
と表される.
|