|
IGModel-SW 1.0
|
|
IGModel-SW 1.0
|
表面高度場の時間変化量を計算する(連続の式を解く)手続きを提供するモジュール. [詳細]
関数/サブルーチン | |
| subroutine, public | continious_equation_Init (icgrid) |
| continious_equation モジュールの初期化. | |
| subroutine, public | calc_continious_eq_dhdt (DHeightDtN, xy_VelN, xy_HeightN, xy_Htopo, diff_eval) |
| 連続の式の半離散式の右辺を評価し, 全格子点に対して, 表面高度の時間変化率を計算する. | |
変数 | |
| type(Field_IcGrid2D), save | mass_flux |
| 質量フラックスの場を管理する構造型 Field_IcGrid2D の変数. | |
表面高度場の時間変化量を計算する(連続の式を解く)手続きを提供するモジュール.
| subroutine,public continious_equation::calc_continious_eq_dhdt | ( | type(Field_IcGrid2D),intent(inout) | DHeightDtN, |
| type(Field_IcGrid2D),intent(in) | xy_VelN, | ||
| type(Field_IcGrid2D),intent(in) | xy_HeightN, | ||
| type(Field_IcGrid2D),intent(in) | xy_Htopo, | ||
| type(Derivate_Field_IcGrid2D),intent(inout) | diff_eval | ||
| ) |
連続の式の半離散式の右辺を評価し, 全格子点に対して, 表面高度の時間変化率を計算する.
具体的には, このサブルーチンでは, 以下の Tomita, etal(2001) の式(2) の半離散式の右辺を評価する.
![\[ \left(\DP{h}{t}\right)_n = - \nabla \cdot ( h_n - h_s ) \Dvect{v}_n \]](form_0.png)
ここで, 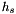 は下部境界における地形の高度場であり, 添字の
は下部境界における地形の高度場であり, 添字の 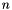 はタイムレベル n の物理場であることを表す.
はタイムレベル n の物理場であることを表す.
| [in,out] | DHeightDtN | タイムレベル n の表面高度場の時間変化率を管理する構造型 Field_IcGrid2D の変数. |
| [in] | xy_VelN | タイムレベル n の速度場を管理する構造型 Field_IcGrid2D の変数. |
| [in] | xy_HeightN | タイムレベル n の表面高度場を管理する構造型 Field_IcGrid2D の変数. |
| [in] | xy_Htopo | 下部境界の高度場を管理する構造型 Field_IcGrid2D の変数. |
| [in] | diff_eval | 正二十面格子上の物理場の微分演算に対するデータを管理する構造型 Derivate_Field_IcGrid2D の変数. |
continious_equation.f90 の 148 行で定義されています。

| subroutine,public continious_equation::continious_equation_Init | ( | type(IcGrid2D_FVM),intent(inout) | icgrid | ) |
continious_equation モジュールの初期化.
| [in,out] | icgrid | 構造型 IcGrid2D_FVM の変数. |
continious_equation.f90 の 96 行で定義されています。

| type(Field_IcGrid2D),save continious_equation::mass_flux |
質量フラックスの場を管理する構造型 Field_IcGrid2D の変数.
continious_equation.f90 の 81 行で定義されています。