IGModel-SW 1.0
Functions/Subroutines

sw_equation_solver Module Reference

This module provides the shallow water equations solver. More...

Functions/Subroutines

subroutine, public init_sw_equation_solver (icgrid)
 Initialize the sw_equation_solver module.
subroutine, public temporal_integration (tstep, dt, icgrid)
 Performs time integration of the shallow water equations.
subroutine RungeKutta_fourth_order (xy_VelA, xy_VelN, DVelDtN, xy_HeightA, xy_HeightN, DHeightDtN, dt, icgrid, idMin)
 Performs time integration of the shallow water equations using the forth-order Runge=Kutta method.
subroutine Adams_Bashforth_third_order (U_nplus1, U_n, dUdt_n, dUdt_nminus1, dUdt_nminus2, dt)
 Performs time integration of the shallow water equations using the third-order Adams-Bashforth method.

Detailed Description

This module provides the shallow water equations solver.



Copyright (C) GFD Dennou Club, 2011-2012. All rights reserved.
license ??

Author:
Yuta Kawai

Function/Subroutine Documentation

subroutine sw_equation_solver::Adams_Bashforth_third_order ( real(DP),dimension(:,:,:,:),intent(inout)  U_nplus1,
real(DP),dimension(:,:,:,:),intent(in)  U_n,
real(DP),dimension(:,:,:,:),intent(in)  dUdt_n,
real(DP),dimension(:,:,:,:),intent(in)  dUdt_nminus1,
real(DP),dimension(:,:,:,:),intent(in)  dUdt_nminus2,
real(DP),intent(in)  dt 
) [private]

Performs time integration of the shallow water equations using the third-order Adams-Bashforth method.

In this subroutine, the future physical fields at 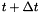$t+\Delta t$(time level n+1) will be predicted in terms of the fields at current time level n and the local time derivatives of fields at current and previous time levels(n, n-1, n-2).

The value of fields at time level n+1 at all grid-points will be predicted using the equation as

\[ \Dvect{U}_{n+1} = \Dvect{U}_n + \dfrac{1}{12} \Delta t \left[ 23 \left(\DP{\Dvect{U}}{t}\right)_{n} - 16 \left(\DP{\Dvect{U}}{t}\right)_{n-1} + 5 \left(\DP{\Dvect{U}}{t}\right)_{n-2} \right] \]

Parameters:
[in,out]U_nplus1The array in which the physical field data at time level n+1 is stored.
[in]dUdt_nThe array in which the local time derivative data of the physical field at time level n is stored.
[in]dUdt_nminus1The array in which the local time derivative data of the physical field at time level n-1 is stored.
[in]dUdt_nminus2The array in which the local time derivative data of the physical field at time level n-2 is stored.
[in]dtTime step [s].

Definition at line 469 of file sw_equation_solver.f90.

Here is the caller graph for this function:

subroutine,public sw_equation_solver::init_sw_equation_solver ( type(IcGrid2D_FVM),intent(inout)  icgrid)

Initialize the sw_equation_solver module.

Parameters:
[in,out]icgridThe variable of derived type IcGrid2D_FVM.

Definition at line 103 of file sw_equation_solver.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

subroutine sw_equation_solver::RungeKutta_fourth_order ( real(DP),dimension(:,idmin:,idmin:,:),intent(inout)  xy_VelA,
real(DP),dimension(:,idmin:,idmin:,:),intent(in)  xy_VelN,
real(DP),dimension(:,idmin:,idmin:,:),intent(inout)  DVelDtN,
real(DP),dimension(:,idmin:,idmin:,:),intent(inout)  xy_HeightA,
real(DP),dimension(:,idmin:,idmin:,:),intent(in)  xy_HeightN,
real(DP),dimension(:,idmin:,idmin:,:),intent(inout)  DHeightDtN,
real(DP),intent(in)  dt,
type(IcGrid2D_FVM),intent(in)  icgrid,
integer,intent(in)  idMin 
) [private]

Performs time integration of the shallow water equations using the forth-order Runge=Kutta method.

In this subroutine, the future physical fields at 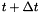$t+\Delta t$(time level n+1) will be predicted in terms of the fields at current time level n.

The future physical field will be predicted using the following equation as

\[ \Dvect{V}_{n+1} = \Dvect{V}_n + \dfrac{\Dvect{k}_1 + 2\Dvect{k}_2 + 2\Dvect{k}_3 + \Dvect{k}_4}{6} \]

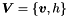Where $ \Dvect{V} = \{\Dvect{v}, h\} $ is a set of variables of velocity and surface height field. 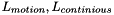$ L_{motion}, L_{continious} $ are functions which represent righ-hand sides of semi-discrete equation of motion, and continious equation, respectively. Then, a set of the functions is defined as 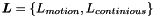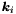$\Dvect{L}=\{ L_{motion}, L_{continious} \} $. $\Dvect{k}_i$ are defined as

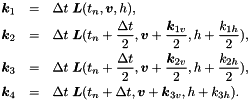
\begin{eqnarray*} \Dvect{k}_1 &=& \Delta t \; \Dvect{L}(t_n, \Dvect{v}, h), \\\ \Dvect{k}_2 &=& \Delta t \; \Dvect{L}(t_n + \dfrac{\Delta t}{2}, \Dvect{v}+\dfrac{\Dvect{k}_{1v}}{2}, h+\dfrac{k_{1h}}{2}) , \\\ \Dvect{k}_3 &=& \Delta t \; \Dvect{L}(t_n + \dfrac{\Delta t}{2}, \Dvect{v}+\dfrac{\Dvect{k}_{2v}}{2}, h+\dfrac{k_{2h}}{2}) , \\\ \Dvect{k}_4 &=& \Delta t \; \Dvect{L}(t_n+\Delta t, \Dvect{v}+\Dvect{k}_{3v}, h+k_{3h}). \end{eqnarray*}

Parameters:
[in,out]xy_VelAThe array in which the velocity field data at time level n+1 is stored.
[in]xy_VelNThe array in which the velocity field data at time level n is stored.
[in,out]DVelDtNThe array in which the time rate of change of velocity field data at time level n is stored.
[in,out]h_nplus1The array in which the surface height field data at time level n+1 is stored.
[in]h_nThe array in which the surface height field data at time level n is stored.
[in,out]dhdt_nThe array in which the time rate of change of surface height field data at time level n is stored.
[in]dtTime step [s].
[in]icgridThe variable of derived type IcGrid2D_FVM.
[in]idMinThe lower bound index of arrays in which various physical fields data is stored.

Definition at line 299 of file sw_equation_solver.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

subroutine,public sw_equation_solver::temporal_integration ( integer,intent(in)  tstep,
real(DP),intent(in)  dt,
type(IcGrid2D_FVM),intent(in)  icgrid 
)

Performs time integration of the shallow water equations.

Parameters:
[in]tstepThe number of time step.
[in]dtTime step.
[in]icgridThe variable of derived type IcGrid2D_FVM.

Definition at line 137 of file sw_equation_solver.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

 All Classes Namespaces Files Functions Variables