|
IGModel-SW 1.0
|
|
IGModel-SW 1.0
|
IGModel-SW は, 主に Tomita, etal(2001) をもとにして作成した, 正二十面体格子による全球浅水モデルである.
Copyright (C) GFD Dennou Club, 2011-2012. All rights reserved.
license ??
![\[ \DP{\Dvect{v}}{t} + ( \zeta + f ) \Dvect{k} \times \Dvect{v} = - \nabla \left( gh + \dfrac{\Dvect{v} \cdot \Dvect{v}}{2} \right) \]](form_3.png)
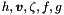 はそれぞれ, 流体の表面高度, 速度ベクトル, 相対渦度, 惑星渦度, 重力加速度である. また,
はそれぞれ, 流体の表面高度, 速度ベクトル, 相対渦度, 惑星渦度, 重力加速度である. また, 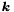 は地理座標系における鉛直方向の単位ベクトルである.
は地理座標系における鉛直方向の単位ベクトルである.
![\[ \DP{h}{t} + \nabla \cdot ( h - h_s ) \Dvect{v} = 0 \]](form_6.png)
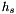 は下部地形の高度である.
は下部地形の高度である.