|
空間微分は 2 次中央差分で離散化する. 時間積分は放射加熱項は前進差分,
拡散項の計算は Crank-Nicolson 法で行う.
放射伝達方程式と拡散方程式の具体的な離散化方法は,
付録 B.d 節, 付録 B.e 節
に示したものと同じである.
鉛直格子の配置と格子間隔は 本文 2.b 節
に示した 2 次元モデルのそれと同じである.
時間刻みは 30 秒とした. 大気上端の入射太陽放射量は北半球夏
(Ls = 100°) の北緯 20°の条件で日変化させる.
大気の初期条件は 220 K 等温, 地中温度は 210 K 一定を初期値とする.
計算時間は 30 日である.
計算された LT = 06:00 における気温と地中の温度分布を
図 C1 , 図 C2 ,
に示す. これらの結果を 本文 2.b 節
で触れた 2 次元モデルの基本場の温度分布として用いる.
大気温度の初期条件を低温側 (160 K 等温)
に設定しても計算される温度分布はほとんど変わらない
(図 C3, 図 C4).
30 日目の気温分布の日変化の様子を 図 C5 に,
地中温度と地表面温度, 地表気温の日変化の様子を 図 C6
に示す.
|
|
|
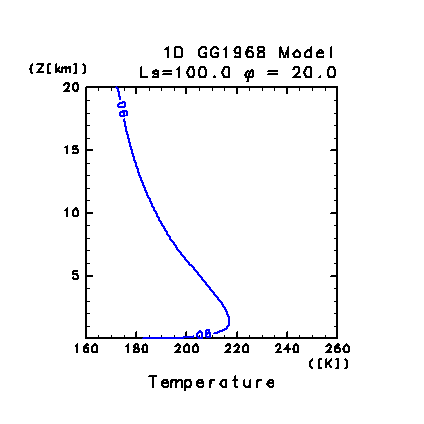
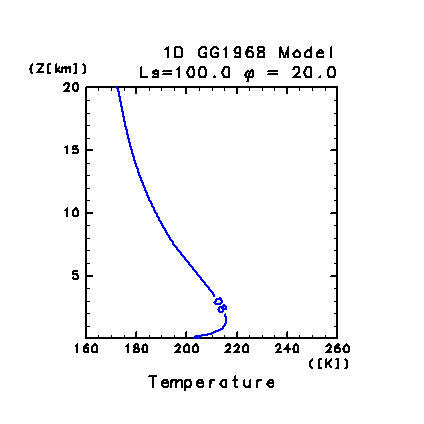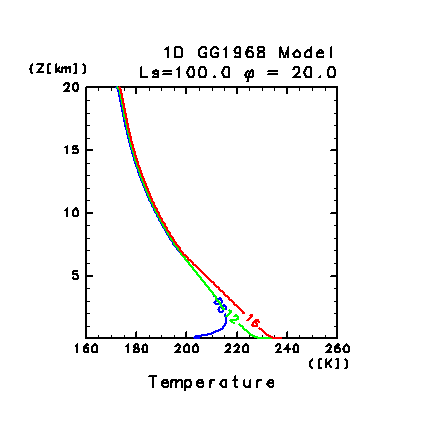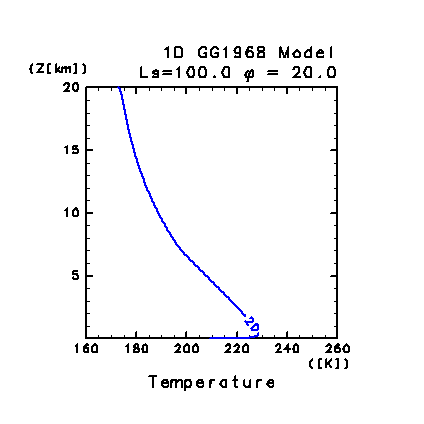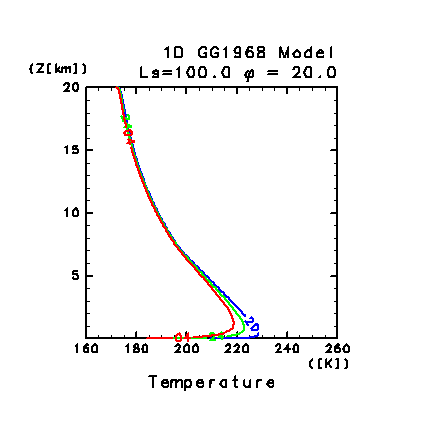
図 C1: 鉛直 1 次元モデルによって計算された 30 日目
LT = 06:00 の大気温度分布.
|
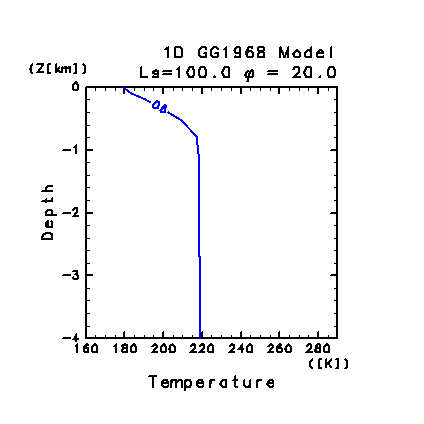
図 C2: 鉛直 1 次元モデルによって計算された 30 日目
LT = 06:00 の地中温度分布. 縦軸の深さは日変化の表皮深さの単位で示してある.
|
|
|
|
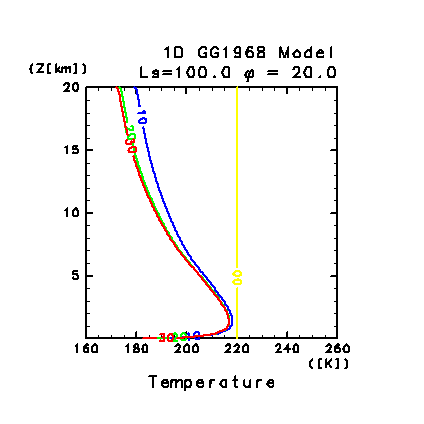
図 C3: 鉛直 1 次元モデルによって計算された大気温度分布の時間変化.
初期温度分布を 220 K 等温とした場合.
LT = 06:00 の温度分布を 10 日毎に表示. 図中の数字は計算日数を表す.
|
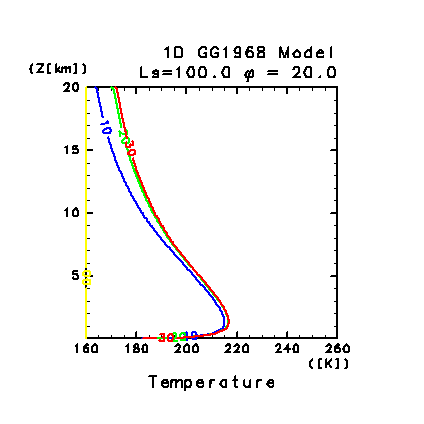
図 C4: 鉛直 1 次元モデルによって計算された大気温度分布の時間変化.
初期温度分布を 160 K 等温とした場合.
LT = 06:00 の温度分布を 10 日毎に表示. 図中の数字は計算日数を表す.
|
|
|
図 C5: 鉛直 1 次元モデルによって計算された
30 日目の大気温度分布の日変化. 図中の数字は時刻を表す.
|
|
|
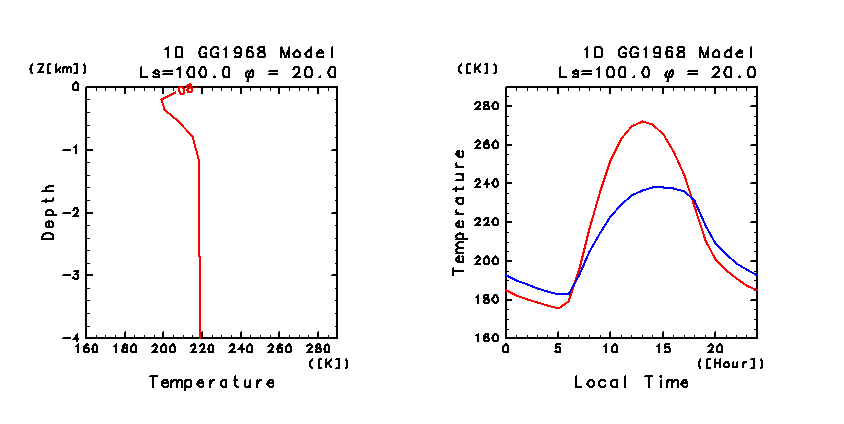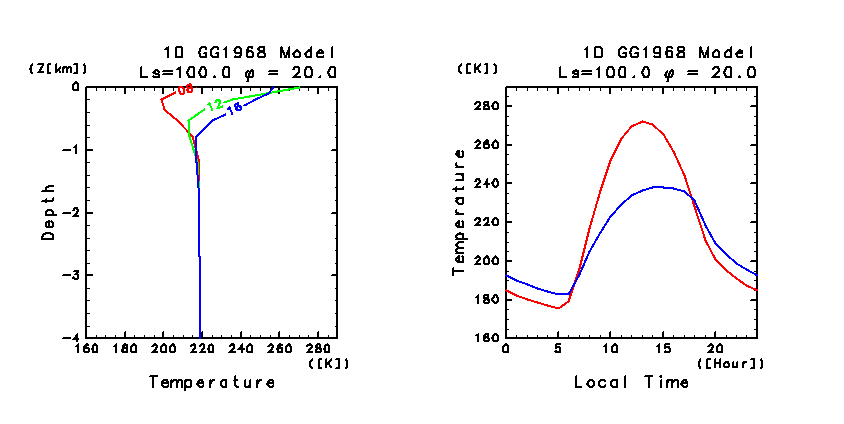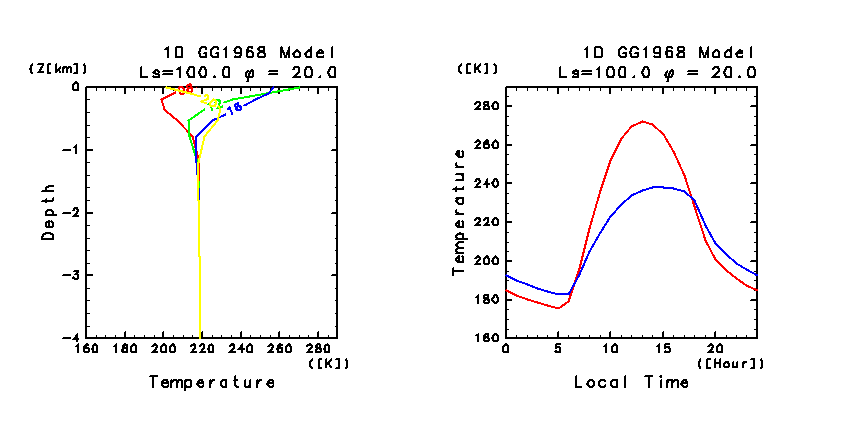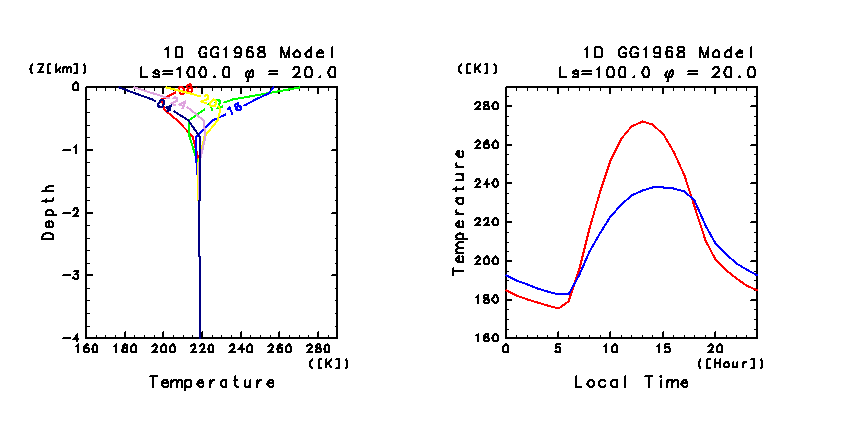
図 C6:
鉛直 1 次元モデルによって計算された
(左)30 日目の地中温度の日変化. LT = 08:00 〜 翌朝 04:00 まで 4 時間毎の結果.
図中の数字は時刻を表す. 縦軸の深さは日変化の表皮深さの単位で示してある.
(右)30 日目の地表面温度と地表気温 の日変化.
1 時間毎の結果. 赤は地表面温度, 青は高度約 1.5 m の気温.
|
|