|
2. 数値モデル |



|
|
- 計算領域と空間分解能
(図 1 参照)
- 大気部分の計算領域は水平に 51.2 km, 鉛直に 20 km である.
ただし放射計算を正確に行うために,
温度場だけを計算する層を大気部分の領域外に 1 層追加する.
水平格子間隔は 100 m, 鉛直格子間隔は高度 100 m 以上では 100 m,
高度 100 m 以下には z = 50, 25 ,12.5, 6.25, 3.125 m に鉛直格子点をとる.
スタッガード格子のためモデル最下層の水平風は高度約 1.5 m で評価される.
100 m という格子間隔は分解能を変えたいくつかの予備的計算によって決定した.
地面の鉛直計算領域は日変化の表皮深さ δd の 6 倍までとり,
鉛直格子間隔は不等である. 具体的な格子点の場所は
z/δd
= -0.1, -0.2, -0.35, -0.53, -0.79, -1.2, -1.8, -2.7, -4.0, -6.0 である
(δd
の大きさについては 付録 A.e 節 を参照).
- 境界条件
- 大気部分の境界条件は水平に周期境界条件, 下部境界では鉛直風を 0,
上部境界は応力無し条件を置く. 上部境界付近の高度 17 km 以上では
対流により励起される重力波を減衰させるため
水平風と鉛直風に対する乱流拡散係数に人工的な値を付加した.
人工的に加えた乱流拡散係数の大きさは 1000 m2sec-1
である. 人工的に加えた乱流拡散係数は高度 19 km から 17 km にかけて線形に
0 へ減少させる.
- 日射量の条件
- ダストのある場合, ダストのない場合ともに大気上端の入射太陽放射量は北半球夏
(火星中心黄径 Ls = 100°) の 20°N の条件で日変化させる.
季節条件は北半球の夏至 (Ls = 90°)
付近であり, 緯度はバイキング 1 号の着陸点の緯度 (北緯 22.4°)
に近い.
- 基本場と初期条件
- 大気の基本場として与える温度分布は,
モデルの概要 で示したモデルと同じ物理過程,
パラメータを持つ鉛直 1 次元放射対流モデルを用いて計算した LT = 06:00
時における鉛直温度である.
基本場の密度と圧力は, その温度分布と静水圧の式,
理想気体の状態方程式を用いて計算される.
鉛直 1 次元モデルの詳細と温度分布の計算方法,
実際に基本場として用いた温度分布は 付録 C 節
に示す.
ダストのない場合の初期条件は水平一様温度分布, 静止大気を与える.
鉛直温度分布は上記の基本場の温度分布である.
さらに計算開始直後の対流の発生を容易にするため, 最下層高度
(z = 3.125 m) の格子点に
±3 K の振幅内におさまる温位擾乱を乱数的に加えた.
地中温度は基本場の温度分布を計算した鉛直 1 次元モデルで計算した温度を用いる.
ダストのある場合の初期条件については
本文 4 節 で述べる.
- 時間刻み, 計算実行環境
- 時間刻みは 0.5 秒または 1 秒である.
この大きさはモデル大気中の最も速い内部重力波位相速度
と CFL 条件から決まる時間刻み程度である. ここで
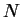 は浮力振動数,
は浮力振動数,
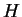 は鉛直計算領域である.
放射加熱(冷却)の計算は 60 秒に 1 回行う.
放射加熱計算の時間格子間隔は,
対流にともなう温度場の変化に放射場が追従できるように決めた.
60 秒という大きさは, 対流にともなう風速のオーダーを 10 msec-1,
対流層の厚さは 1 〜 10 km のオーダーであると仮定すると, 対流にともなう
温度変化の時間スケールが 100 〜 1000 sec 程度となることによる.
は鉛直計算領域である.
放射加熱(冷却)の計算は 60 秒に 1 回行う.
放射加熱計算の時間格子間隔は,
対流にともなう温度場の変化に放射場が追従できるように決めた.
60 秒という大きさは, 対流にともなう風速のオーダーを 10 msec-1,
対流層の厚さは 1 〜 10 km のオーダーであると仮定すると, 対流にともなう
温度変化の時間スケールが 100 〜 1000 sec 程度となることによる.
計算実行は
京都大学大型計算機センター,
および
文部省宇宙科学研究所宇宙科学企画情報解析センター
にある富士通 VPP800 システムにおいて行った.
必要な計算機資源は主記憶約 256 メガバイト, 時間格子間隔 0.5 秒で
24 時間計算を行う場合の CPU 時間は約 8 時間である.
|
2次元非弾性系を用いた火星大気放射対流の数値計算
Odaka, Nakajima, Ishiwatari, Hayashi,
Nagare Multimedia 2001
|



|
|