|
火星探査衛星バイキングの着陸船は高度 1.6 m における風と気温を観測した.
本研究で用いた数値モデルの最下層格子点は高度約 1.5 m にあるので, モデ
ル最下層の風と気温をバイキングの観測結果と直接比較することができる.
そこで本研究の数値計算結果を
Hess et al., (1977)
が対流によるものであると指摘したバイキング 1
号着陸点での風と気温の変動
( Hess et al., 1977, 図9)
と比較する.
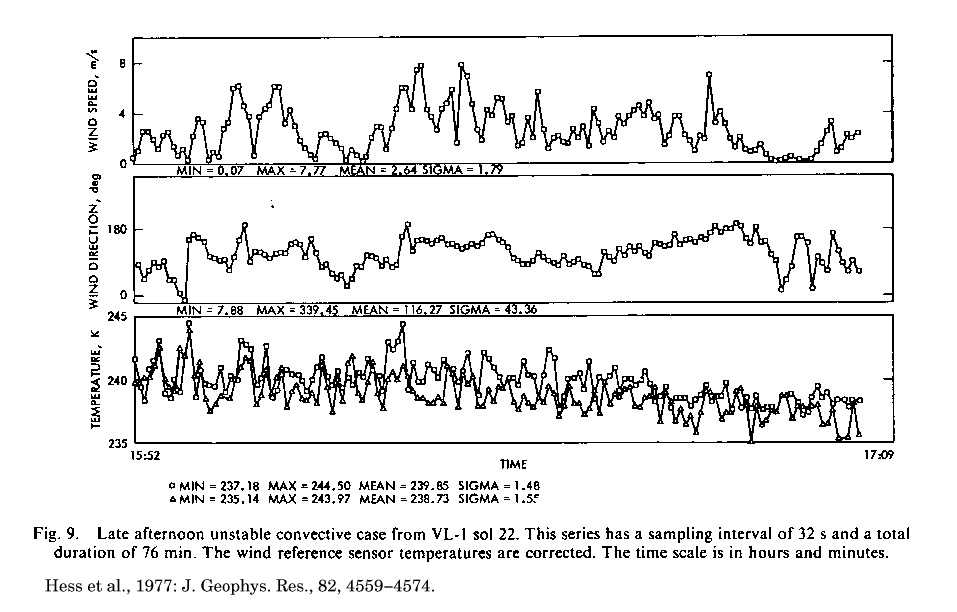
図 15a にバイキング 1 号着陸点において観測
された風速, 風向, 気温の時系列を示す. 観測日時は着陸後 22 日目
(Ls 〜 110°) の LT = 15:52 〜 17:09 である.
この時の火星大気中のダストの可視光に対する光学的厚さは約 0.4
(Pollack et al., 1979) である.
これは本研究において計算した「ダストのない場合」と「ダストのある場合」の
中間的な値である.
観測された風速には 5 msec-1 程度の振幅を持ち
数分から十数分の時間スケールで変動する成分と,
3 msec-1 程度の振幅を持ち
1 〜 2 分の時間スケールで変動する成分が重なって見られる.
温度の変動にも風と同様に 2 つの時間スケールで変動する成分が見られ,
その振幅は共に 3 K 程度である.
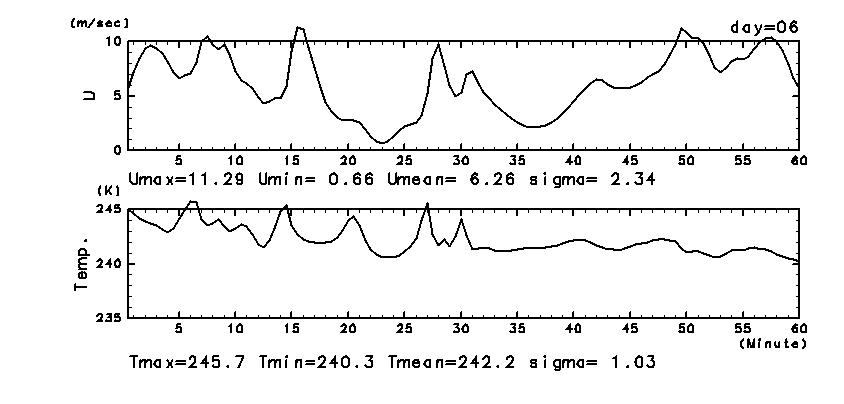
図 15a に示された変動のうち,
風と温度の比較的長い時間スケールの変動の様子は
本研究において計算されたダストのない場合の変動の様子
(図 15b) とよく似ている.
これらの変動は下層から立ち上がるプリュームの根本の通過や,
対流層全体にわたる対流セルの循環にともなうものであると考えられる.
一方観測に見られる短い時間スケールの変動は本研究の計算では再現できていない.
これらの変動は本研究で用いたモデルではパラメタライズされている
100 m 以下の空間スケールを持つ現象,
例えば熱伝導層や遷移層内の熱的あるいは強制乱流
にともなうものであると想像される.
以上より, 本研究の数値計算の結果は
火星大気に実際に存在する放射対流の様子を
微細な乱流構造を除きほぼ再現しており,
逆に, 観測データで示された時間変動のうちの数分から十数分程度の
時間スケールを持つ変動が放射対流によるキロメータサイズの運動によ
るものであると言うことができる.
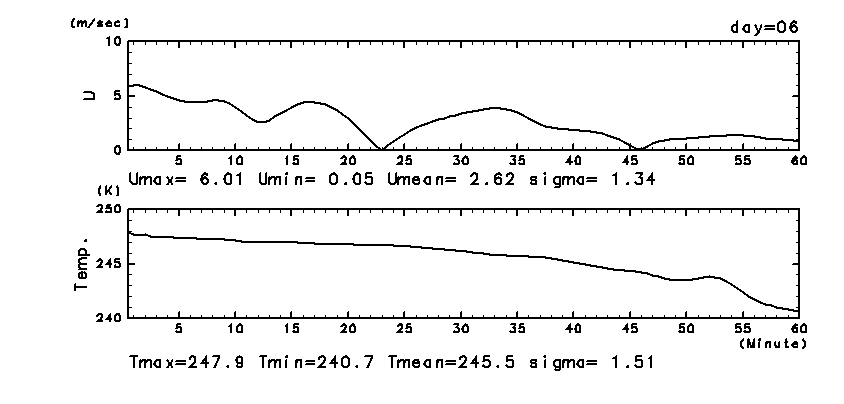
ダストのある場合の計算結果 (図 15c)
には観測に見られるような変動は現われていない.
その主な原因は大気中のダストの量の違いであると考えられる.
バイキングの観測時に比べダストの量が多いため,
成層が安定化し対流の活動が抑制されたと想像される.
実際にこの時間帯では,
数値モデルによって計算された対流の活動はほぼ収束している
(図 13 参照).
|
|
図 15a:
バイキング 1 号着陸点において観測された風速, 風向, 気温の時系列
(Hess et al., 1977, 図9).
着陸後 22 日目 LT = 15:52 〜 17:09 の観測. 出力時間間隔は 32 秒.
|
|
|
図 15b:
2 次元モデルによって計算された風速, 気温の時系列.
ダストのない場合の 6 日目の LT = 16:00 〜 17:00 の結果.
出力時間間隔は 30 秒.
|
|
|
図 15c:
2 次元モデルによって計算された風速, 気温の時系列.
ダストの巻き上げ後 6 日目の LT = 16:00 〜 17:00 の結果.
出力時間間隔は 30 秒.
気温の時系列の横軸範囲は 図 14a,
図 14b とは異なることに注意.
|
|