|
本研究から予想されることは,
キロメータサイズの対流にともなう風のゆらぎをきちんと考慮してあげれば,
ダストのない初期条件から出発した GCM
シミュレーションにおいてもダストを地表面から巻き上げることが可能になるであろう,
ということである.
これまでの火星大気 GCM
で用いられている標準的な対流パラメタリゼーションは対流調節スキームである.
対流調節は熱的に不安定な場を対流による熱輸送の結果到達するであろう
熱的に中立安定な場へと調節する.
対流調節にしろ他のパラメタリゼーションにしろ,
キロメータサイズの対流にともなう風のゆらぎとそれによる地表面摩擦応力への寄与は
全く考慮されていない.
これまでは火星の鉛直対流構造に関する知見が無かったので,
火星大気 GCM では対流調節を用いるしか方法はなかった.
火星大気におけるキロメータサイズの対流に対応する地球大気の現象,
すなわち, 対流圏全体に地表面からの熱を第一義的に伝える現象は積雲対流である.
地球大気 GCM においては積雲対流を適切に表現するために,
さまざまな積雲対流パラメタリゼーションが開発されてきた.
その最も簡単な表現は対流調節であり,
複雑なものでは積雲の鉛直サイズ分布, 積雲内へのエントレインメント
等を考慮している
(例えば Arakawa and Schubert, 1974).
積雲対流パラメタリゼーションの開発が可能であったのは,
観測と理論によって積雲対流の具体的な描像がある程度把握されていたからである.
しかしこれらの積雲対流パラメタリゼーションで重要視されていた問題は
積雲対流による鉛直熱輸送であり, 風のゆらぎではない.
風のゆらぎを考慮する対流パラメタリゼーションは, これまでの地球大気
GCM においてはその必要もあまり無かったため検討されてこなかった問題である.
本研究によって火星大気の鉛直対流の具体的イメージが明確になり,
それがキロメータサイズの対流であることが明らかにされた.
GCM における地表面応力は,
モデル中で陽に計算される風の強度を用いていわゆるバルク法という定式化によってパラメタライズされている.
本研究で用いた数値モデルにおいても地表面応力はバルク法に基づいて計算されている.
にもかかわらず, 本研究の数値モデルにおいては
GCM による計算よりも大きな地表面応力の値が得られている.
これはまさにキロメータサイズの対流を陽に計算したことの結果である.
図 5 および
図 6 より,
本研究での計算においても平均値としてはそれほど大きな地表面応力が得られているわけではない.
しかし, キロメータサイズの対流にともない地表面風速に大きな変動があるために,
地表面応力の値は局所的に平均値よりもずっと大きくなり得るのである.
GCM で用いられるパラメタリゼーションが表現する地表面応力は,
たとえサブグリッドスケールの色々なスケールの乱流 (キロメートル
サイズの渦も含むような) の効果が算入されるにしても,
あくまで広い領域 (GCM の水平格子サイズの) で平均した値である.
したがってその値は本研究で得られた応力の水平平均値に対応するものであり,
局所的に現れる極大値より小さくならざるを得ない.
数値計算によって示されたキロメータサイズの対流の描像を基に,
対流にともなう風のゆらぎとそれに伴う地表面応力の最大値を
評価できるような対流パラメタリゼーションを考察することができるだろう.
その概要は,
対流調節に対流運動エネルギーの評価スキームを追加したようなものになる.
対流運動エネルギーは温位のゆらぎ 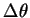 と対流層の厚さ と対流層の厚さ 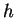 を用いて
(1)
のような形式でただちに評価することができる.
地表面付近の乱流拡散係数の大きさを仮定すれば
(たとえば GCM での最下層で評価される値をそのまま用いるか, または, を用いて
(1)
のような形式でただちに評価することができる.
地表面付近の乱流拡散係数の大きさを仮定すれば
(たとえば GCM での最下層で評価される値をそのまま用いるか, または,
 = 15
m2sec-1 等とする),
本文 3.d. 節
での議論から, 対流で輸送されるべき熱フラックス = 15
m2sec-1 等とする),
本文 3.d. 節
での議論から, 対流で輸送されるべき熱フラックス
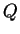 を GCM の出力値から与えて を GCM の出力値から与えて
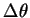 を評価することができる.
これらを用いることによりキロメータサイズの対流の風速変動のスケールを推定する事ができる.
このようにして推定された風速の変動幅を
地表フラックスパラメタリゼーション
の計算式において考慮することによって,
GCM 内において自然にダストの巻き上げが表現されることになるであろう. を評価することができる.
これらを用いることによりキロメータサイズの対流の風速変動のスケールを推定する事ができる.
このようにして推定された風速の変動幅を
地表フラックスパラメタリゼーション
の計算式において考慮することによって,
GCM 内において自然にダストの巻き上げが表現されることになるであろう.
|