|
3.d. 対流の強度 (2): 乱流拡散による熱伝導層
|
高度 50 m 以下の領域の温位勾配は乱流拡散によって決まる温位勾配,
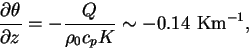 |
(2) |
とよい一致を示す. ここで 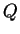 は熱フラックスである.
(2) の見積もりに際し
ては, 正午付近の赤外放射と顕熱による加熱の合計値 は熱フラックスである.
(2) の見積もりに際し
ては, 正午付近の赤外放射と顕熱による加熱の合計値 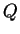 〜 30 Wm-2, 〜 30 Wm-2,
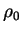 = 2×10-2 kgm-3, = 2×10-2 kgm-3,  = 734.9
Jkg-1K-1, = 734.9
Jkg-1K-1,  に数値モデルで計算された乱流拡散係数の値 15
m2sec-1 を代入した.
したがって高度 50 m 以下の領域は熱伝導層と呼ぶことができる. に数値モデルで計算された乱流拡散係数の値 15
m2sec-1 を代入した.
したがって高度 50 m 以下の領域は熱伝導層と呼ぶことができる.
熱伝導層の温度構造が (2) 式で与えられる場合,
熱伝導層の厚さ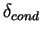 と層内の温位差 と層内の温位差 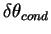 がどの程度の大きさになるかを見積もることにする.
熱伝導層のフラックスレイリー数
がどの程度の大きさになるかを見積もることにする.
熱伝導層のフラックスレイリー数
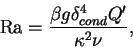 |
(3) |
がある値を越えると熱的不安定が生じると想像される. ここで 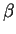 は熱膨張
係数, は熱膨張
係数, 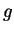 は重力加速度, は重力加速度, 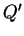 は温度フラックス( は温度フラックス(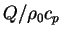 ), ),
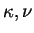 はそれぞれ熱拡散係数, 動粘性係数である. はそれぞれ熱拡散係数, 動粘性係数である. 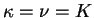 , ,
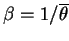 とすると, 熱伝導層の厚さ とすると, 熱伝導層の厚さ 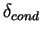 は式から以下のように与えられる.
は式から以下のように与えられる.
 |
(4) |
数値を代入する際には (2) 式を利用した.
線形安定性解析から求められるフラックス固定の場合の臨界レイリー数のオーダーは
100 程度であることが知られている
(Sasaki, 1970). この場合, 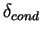 〜 57 m となり, 層内の温位差 〜 57 m となり, 層内の温位差
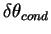 は (2) 式より約 8 K となる.
図 7 に示された
LT = 14:00 における熱伝導層の厚さと温位差はこれらの値に比べやや小さいが
(
は (2) 式より約 8 K となる.
図 7 に示された
LT = 14:00 における熱伝導層の厚さと温位差はこれらの値に比べやや小さいが
(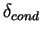 < 50 m, < 50 m, 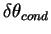 〜 6 K), およその大きさは評価されていると言える. 〜 6 K), およその大きさは評価されていると言える.
|