|

|
|
図 8: 鉛直 1 次元の「煙突」対流プリュームモデル.
|
対流の強度 (2) での考察により,
日中の熱伝導層内の温位差はおよそ数 K 程度になることが予想される.
しかし対流層内のプリュームが持つ温位差は 2 K 程度である.
この違いは熱伝導層と対流層とに挟まれた温位がゆるやかに変化する領域において,
上昇するプリュームによる周囲の相対的に冷たい空気の取り込み
(エントレインメント) が発生するためである.
以下ではこのエントレインメントの発生している領域を遷移層と呼ぶことにする.
エントレインメントによるプリュームの温位差への影響が
どのように表されるかを考察する. 図 8
青線枠内に示すようなプリュームの根の部分において, 遷移層の下方から温位 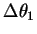 の空気が の空気が 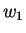 の速度で流入し, 温位
の速度で流入し, 温位 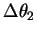 の空気が
の空気が 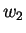 の速度で対流層へ流出すると考える. 温度のバランスを考えると,
の速度で対流層へ流出すると考える. 温度のバランスを考えると,
となる. 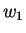 は熱伝導層から上昇したプリュームの持つ浮力と熱伝導層の乱流拡散時間
は熱伝導層から上昇したプリュームの持つ浮力と熱伝導層の乱流拡散時間 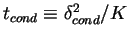 から見積もり,
から見積もり, 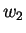 は対流層内のプリュームによってなされる浮力仕事から見積もる.
は対流層内のプリュームによってなされる浮力仕事から見積もる.
ここで 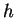 は対流層全体の厚さである.
熱伝導層で生成されたプリュームがその温位差を保ったまま対流層を移動する時間
は対流層全体の厚さである.
熱伝導層で生成されたプリュームがその温位差を保ったまま対流層を移動する時間
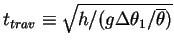 を定義すると, を定義すると,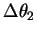 は は
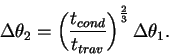 |
(5) |
と表される. エントレインメントの影響の程度はプリュームの移動時間に対する
乱流拡散時間の比によって決まることになる.
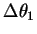 を熱伝導層の持つ温位差とし, 対流層内のプリュームの温位差
を熱伝導層の持つ温位差とし, 対流層内のプリュームの温位差
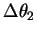 を (5)
式を用いて評価してみよう. 日中の LT = 14:00 を想定し,
図 7 より
を (5)
式を用いて評価してみよう. 日中の LT = 14:00 を想定し,
図 7 より 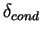 〜 40 m,
〜 40 m, 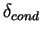 〜 6 K とする. このとき,
〜 6 K とする. このとき,
となる. この 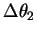 の見積もりは LT=14:00 のプリュームの持つ温位差にだいたい一致する.
の見積もりは LT=14:00 のプリュームの持つ温位差にだいたい一致する.
以上の考察から, 熱フラックス 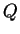 ,
乱流拡散係数 ,
乱流拡散係数  ,
対流層の厚さ ,
対流層の厚さ 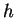 とを与えると,
熱境界層と対流プリュームの持つ温位差をほぼ記述できることがわかった.
ただし
とを与えると,
熱境界層と対流プリュームの持つ温位差をほぼ記述できることがわかった.
ただし 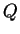 に含まれる顕熱による加熱量,
乱流拡散係数は運動そのものによって決められている.
したがって対流場全体の因果関係を説明したわけではないことに注意が必要である.
に含まれる顕熱による加熱量,
乱流拡散係数は運動そのものによって決められている.
したがって対流場全体の因果関係を説明したわけではないことに注意が必要である.
(5)
式によるプリュームの持つ温位差の見積もりは, 対流がよく発達し, 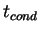 <
<  であるような場合に適用できることに注意したい.
であるような場合に適用できることに注意したい. 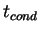 >
>  の場合には
の場合には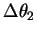 >
>
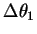 となり熱伝導層の持つ温位差よりもプリュームの持つ温位差が大きくなる
というおかしな結果が得られてしまう.
この場合はエントレインメントはほとんど起こらないと考えるのが自然である.
となり熱伝導層の持つ温位差よりもプリュームの持つ温位差が大きくなる
というおかしな結果が得られてしまう.
この場合はエントレインメントはほとんど起こらないと考えるのが自然である.
|