|
IGModel-SW 1.0
|
|
IGModel-SW 1.0
|
浅水方程式ソルバを提供するモジュール. [詳細]
関数/サブルーチン | |
| subroutine, public | init_sw_equation_solver (icgrid) |
| sw_equation_solver モジュールの初期化を行う. | |
| subroutine, public | temporal_integration (tstep, dt, icgrid) |
| 浅水方程式系の時間積分を行う. | |
| subroutine | RungeKutta_fourth_order (xy_VelA, xy_VelN, DVelDtN, xy_HeightA, xy_HeightN, DHeightDtN, dt, icgrid, idMin) |
| 4 次の Runge=Kutta 法を用いて, 浅水方程式系を時間積分する. | |
| subroutine | Adams_Bashforth_third_order (U_nplus1, U_n, dUdt_n, dUdt_nminus1, dUdt_nminus2, dt) |
| 3 次の Adams=Bashforth 法を用いて, 浅水方程式系を時間積分する. | |
浅水方程式ソルバを提供するモジュール.
Copyright (C) GFD Dennou Club, 2011-2012. All rights reserved.
license ??
| subroutine sw_equation_solver::Adams_Bashforth_third_order | ( | real(DP),dimension(:,:,:,:),intent(inout) | U_nplus1, |
| real(DP),dimension(:,:,:,:),intent(in) | U_n, | ||
| real(DP),dimension(:,:,:,:),intent(in) | dUdt_n, | ||
| real(DP),dimension(:,:,:,:),intent(in) | dUdt_nminus1, | ||
| real(DP),dimension(:,:,:,:),intent(in) | dUdt_nminus2, | ||
| real(DP),intent(in) | dt | ||
| ) | [private] |
3 次の Adams=Bashforth 法を用いて, 浅水方程式系を時間積分する.
このサブルーチンでは, 現在の時刻 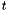 (タイムレベル n )の物理場の値と, タイムレベル n,n-1,n-2 の物理場の局所時間微分を用いて, 時刻
(タイムレベル n )の物理場の値と, タイムレベル n,n-1,n-2 の物理場の局所時間微分を用いて, 時刻 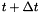 (タイムレベル n+1 )の未来の物理場の値を予報する.
(タイムレベル n+1 )の未来の物理場の値を予報する.
全格子点におけるタイムレベル n+1 の物理場 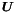 の値は, 以下の式によって予測される.
の値は, 以下の式によって予測される.
![\[ \Dvect{U}_{n+1} = \Dvect{U}_n + \dfrac{1}{12} \Delta t \left[ 23 \left(\DP{\Dvect{U}}{t}\right)_{n} - 16 \left(\DP{\Dvect{U}}{t}\right)_{n-1} + 5 \left(\DP{\Dvect{U}}{t}\right)_{n-2} \right] \]](form_21.png)
| [in,out] | U_nplus1 | タイムレベル n+1 の物理場データを保持する配列. |
| [in] | dUdt_n | タイムレベル n の物理場の局所時間微分データを保持する配列. |
| [in] | dUdt_nminus1 | タイムレベル n-1 の物理場の局所時間微分データを保持する配列. |
| [in] | dUdt_nminus2 | タイムレベル n-2 の物理場の局所時間微分データを保持する配列. |
| [in] | dt | 時間刻み幅 [s]. |
sw_equation_solver.f90 の 469 行で定義されています。

| subroutine,public sw_equation_solver::init_sw_equation_solver | ( | type(IcGrid2D_FVM),intent(inout) | icgrid | ) |
sw_equation_solver モジュールの初期化を行う.
| [in,out] | icgrid | 構造型 FVIcGrid2D_FVM変数. |
sw_equation_solver.f90 の 103 行で定義されています。


| subroutine sw_equation_solver::RungeKutta_fourth_order | ( | real(DP),dimension(:,idmin:,idmin:,:),intent(inout) | xy_VelA, |
| real(DP),dimension(:,idmin:,idmin:,:),intent(in) | xy_VelN, | ||
| real(DP),dimension(:,idmin:,idmin:,:),intent(inout) | DVelDtN, | ||
| real(DP),dimension(:,idmin:,idmin:,:),intent(inout) | xy_HeightA, | ||
| real(DP),dimension(:,idmin:,idmin:,:),intent(in) | xy_HeightN, | ||
| real(DP),dimension(:,idmin:,idmin:,:),intent(inout) | DHeightDtN, | ||
| real(DP),intent(in) | dt, | ||
| type(IcGrid2D_FVM),intent(in) | icgrid, | ||
| integer,intent(in) | idMin | ||
| ) | [private] |
4 次の Runge=Kutta 法を用いて, 浅水方程式系を時間積分する.
このサブルーチンでは, 時刻 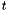 (タイムレベル n )の物理場の値から未来の時刻
(タイムレベル n )の物理場の値から未来の時刻 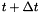 (タイムレベル n+1 )の物理場の値を予報する. 今, 速度場と高度場の変数の組を
(タイムレベル n+1 )の物理場の値を予報する. 今, 速度場と高度場の変数の組を 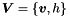 と書くことにする. また,
と書くことにする. また, 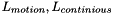 をそれぞれ運動方程式と連続の式の半離散式の右辺を表す関数とし,
をそれぞれ運動方程式と連続の式の半離散式の右辺を表す関数とし, 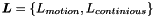 とする. このとき, 以下の式を計算し, 未来の物理場を予報する.
とする. このとき, 以下の式を計算し, 未来の物理場を予報する.
![\[ \Dvect{V}_{n+1} = \Dvect{V}_n + \dfrac{\Dvect{k}_1 + 2\Dvect{k}_2 + 2\Dvect{k}_3 + \Dvect{k}_4}{6} \]](form_17.png)
ここで, 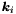 は次のように定義される.
は次のように定義される.
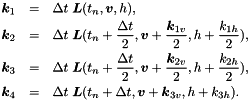
| [in,out] | xy_VelA | タイムレベル n+1 の速度場データを保持する配列. |
| [in] | xy_VelN | タイムレベル n の速度場データを保持する配列. |
| [in,out] | DVelDtN | タイムレベル n の速度場データの時間変化率を保持する配列. |
| [in,out] | h_nplus1 | タイムレベル n+1 の表面高度場データを保持する配列. |
| [in] | h_n | タイムレベル n の表面高度場データを保持する配列. |
| [in,out] | dhdt_n | タイムレベル n の表面高度場の時間変化率のデータを保持する配列. |
| [in] | dt | 時間刻み幅 [s]. |
| [in] | icgrid | 構造型 IcGrid2D_FVM の変数. |
| [in] | idMin | 各種物理場を保持する配列の下限境界インデックス. |
sw_equation_solver.f90 の 299 行で定義されています。


| subroutine,public sw_equation_solver::temporal_integration | ( | integer,intent(in) | tstep, |
| real(DP),intent(in) | dt, | ||
| type(IcGrid2D_FVM),intent(in) | icgrid | ||
| ) |
浅水方程式系の時間積分を行う.
| [in] | tstep | 時間スッテプ数 |
| [in] | dt | 時間刻み幅. |
| [in] | icgrid | 構造型 IcGrid2D_FVM の変数. |
sw_equation_solver.f90 の 137 行で定義されています。

